#数楽 http://www.math.tohoku.ac.jp/~kuroki/LaTeX/20120810FriezePattern.pdf … 黒木玄、「フリーズパターン ―― 数の繰り返し模様の不思議」、仙台数学セミナーのために作った原稿の大幅拡充版。

#数楽 フリーズパターンの出前授業ネタとしての良いところは自然数の足算掛算割算の計算ができれば理解できる話であること。上手にやれば小学生でも理解できると思う。本当はディンキン図形がからむ数学との関係を小学生にもわかるように説明したいのだが、まだ良い方法を思い付かない。

@genkuroki #数楽 フリースパターンの解説文はインターネットで検索すると以下が見つかる： http://tinyurl.com/9dot6j5  http://tinyurl.com/d9xb9mt  http://tinyurl.com/bt7ygzb  http://tinyurl.com/d6x3yeo  続く

@genkuroki #数楽 続き http://tinyurl.com/btezhy3  http://tinyurl.com/cerx35x  。3つ目には「小学生でも理解できる！」と冒頭に書いてあり、6つ目にも子どもにとってよい練習になるというような話がp.19に書いてあります。続く

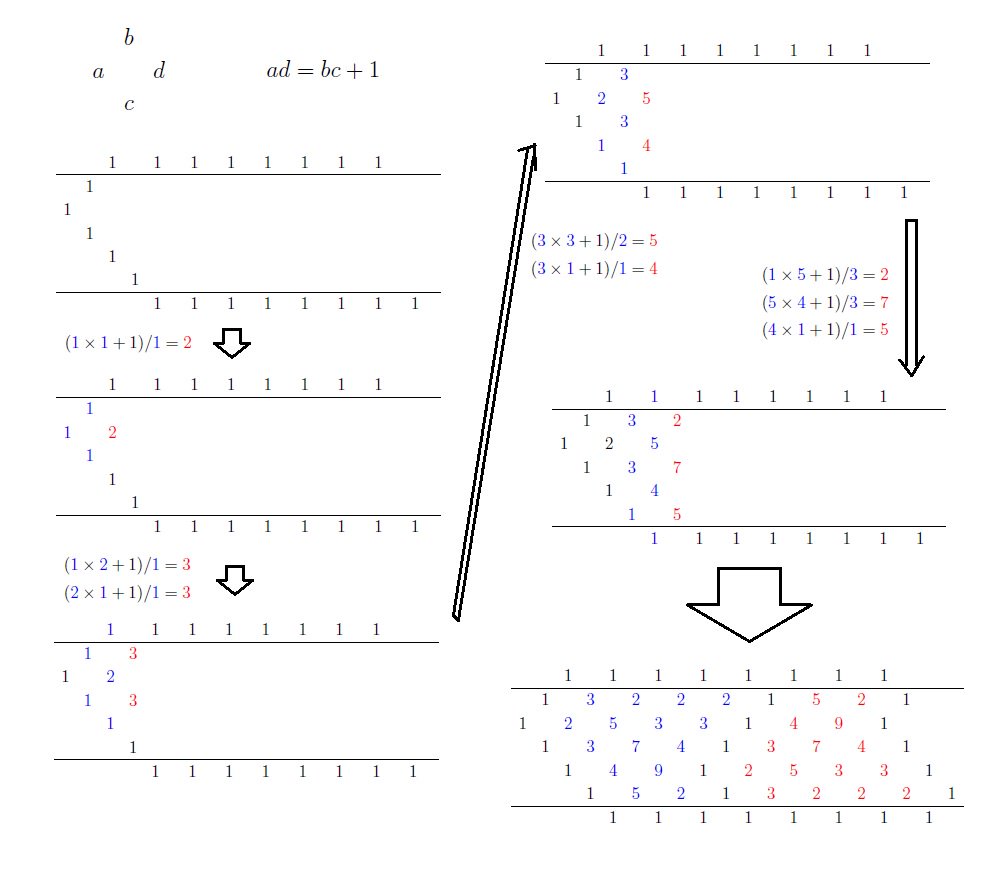
@genkuroki #数楽 続き。数のフリーズ模様を作る手続きは「かけて1をたしてわる」の繰り返しになるのですが、初期条件を1のジグザグにとれは必ず割り切れます(これは一応非自明)。計算ミスをすると割り切れなくなるのですぐに気付けます(これが大事！)。続く

@genkuroki #数楽 続き。実際に計算してみると「あれ～、これって本当に割り切れるのかなあ～」という気持ちになっても割り切れまくる。これは気持ちが良いです。多角形の三角形分割からフリーズパターンを作れることも確認してみると面白いでしょう。続く

@genkuroki #数楽 続き。このフリーズパターンの背景にある数学は21世紀になってクラスター代数の理論として大発展しました。そういう話に繋がる数遊びを小学生でもできるというのはうれしい話だと思います。まとめると、～続く

@genkuroki #数楽 【まとめ：フリーズパターンは以下の特長を持つ。(1)小学生でも遊べる。(2)すべてが割り切れて気持ちがよい。計算ミスをすれば自然に気付く。(3)多角形の三角形分割を使っても作れる。(4)21世紀の数学とも直接に関係している。】流行すると良いと思う。

#数楽 http://bit.ly/V76ZRO  は色々参考になりました。方眼の入った紙を利用していること。色を付けてきれいに見えるように工夫していること。などなど。色鉛筆は常備している家が多いと思いますが、方眼紙の方はそうではないと思う。うちでも常備しておくことにしよう。

#数楽 数学の世界に不思議なことが起こっていることが見えるような子どもにもできる遊びをたくさん集めておくことは大事なことだと思う。古典的なやつでは142857を2～6倍するとどうなるかとか。電卓でやっても面白い。これの仕組みはフリーズパターンよりはずっと簡単。

@genkuroki #数楽 Conway-Coxeterのフリーズパターンで初期条件を「単純な1のジグザグ」(1が上から左下、右下、左下、右下、と並んでいる状態)にすると、フィボナッチ数しか出て来ないことを観察できます。これはConway-Coxeterも問題に出している。

http://cruel.hatenablog.com/entry/2015/12/21/115640 … にあるv.1.3のPDF http://cruel.org/candybox/80sSFfandom.pdf … (500KB)を見て、昔書いた http://www.math.tohoku.ac.jp/~kuroki/LaTeX/20120810FriezePattern.pdf … の見た目を思い出した。そのTeXソースも公開することにした。続く

続きhttp://www.math.tohoku.ac.jp/~kuroki/LaTeX/20120810FriezePattern.pdf … のTeXソース→ http://www.math.tohoku.ac.jp/~kuroki/LaTeX/20120810FriezePattern.tex …画像→ https://en.wikipedia.org/wiki/Frieze_of_Parnassus#/media/File:Albert_Memorial_Friese_Collage_-_May_2008-edit1.jpg …画像のBB→ http://www.math.tohoku.ac.jp/~kuroki/LaTeX/610px-Albert_Memorial_Friese_Collage_-_May_2008-edit1.bb …TeXソースも公開されていると結構便利

#数楽 http://www.math.tohoku.ac.jp/~kuroki/LaTeX/20120810FriezePattern.pdf … (TeXソースは一つ前のツイートにある)の売りは(1)足算掛算割算ができれば誰でも楽しめるフリーズパターンを扱っている。小3レベルの計算練習にぴったり！(2)21世紀の数学であるクラスター代数入門にもなっている。続く

#数楽 http://www.math.tohoku.ac.jp/~kuroki/LaTeX/20120810FriezePattern.pdf … の売りの説明続き(3)A型だけではなく、BCD型も扱っている。(4)EFGの例外型も扱っている。(5)整数性と有限反復性の証明がきちんと説明されている。(6)A型の場合と多角形の三角形分割の関係も説明されている。続く

#数楽 続き(7)ランク2のアフィン型(A^{(1)}_1とA^{(2)}_2)の場合も扱っている。(8)型がsimply-lacedでも対称でもない一般の場合のクラスター変換を(拡張された)箙の図を描いて説明する方法が書いてある。(9)色を使っている。白黒ではない。

#数楽 続き(10) http://www.math.tohoku.ac.jp/~kuroki/LaTeX/#20120817 … でTeXソースが公開されている。(11)TeXソースを見ると画像の挿入の仕方と箙の図の描き方がわかる。などなど。

#数楽 小学生に計算練習をさせるときにも、少しは意味のある計算をしてもらった方がいいのではないかと思う。無意味な計算を延々とするのはつまらない。フリーズパターンはその観点からも優れている。真に面白い数学の一部分だし、次々に全部割り切れる計算は結構快感。

#数楽 http://www.math.tohoku.ac.jp/~kuroki/LaTeX/20120810FriezePattern.pdf … の「売り」に追加(12)foldingについても解説してある。A_{2n-1}→B_n、D_{n+1}→C_n、E_6→F_4、D_4→G_2、A_∞→A_^{(1)}_1

Re:RTs 色々、勉強になった。Colorblind Visionは多分Androidアプリ。iOSなら「色のシミュレータ」というアプリでスクリーンショットの様々な色覚特性での見え方を比較できる。

#数楽 私が書いたもので色を多用したのはこれ→ http://www.math.tohoku.ac.jp/~kuroki/LaTeX/20120810FriezePattern.pdf … フリーズパターン - 数の繰り返し模様の不思議直接読むと高校レベル。誰かに説明してもらえれば小3レベル。なぜか常に割り切れる計算は気持ちが良い。ディンキン図形が出て来る数学。

#数楽 実は書き切った後で色に頼った説明をしたことを後悔した。大量にコピーするときには予算的にカラーコピーしたくないなと感じてしまうから。白黒でコピーしても読めるように書くべきだった。再掲：後悔したのはこれ→ http://www.math.tohoku.ac.jp/~kuroki/LaTeX/20120810FriezePattern.pdf …

#数楽 百マス計算のような無意味な計算をするより、フリーズパターンの計算をした方が楽しいと思う。割り切れなかったり、周期的にならなければ、計算ミスしていることがわかる。http://www.math.tohoku.ac.jp/~kuroki/LaTeX/20120810FriezePattern.pdf …

#数楽 "フリーズパターンの数理"割り算を習った小学生にできる数遊び。次々に割り切れるのが気持ち良い。https://twitter.com/i/moments/850318726628900864 …