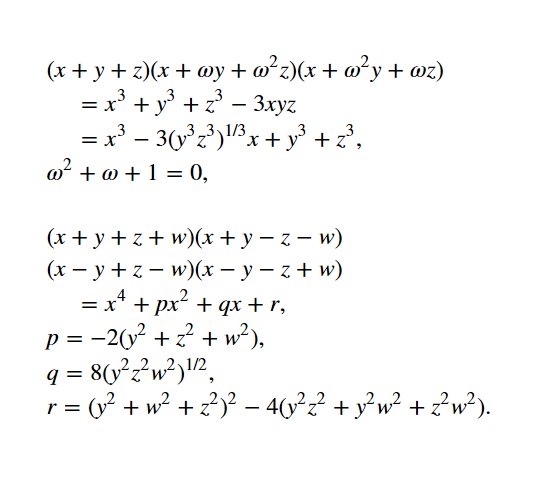因数分解の公式と3次方程式と4次方程式の解法
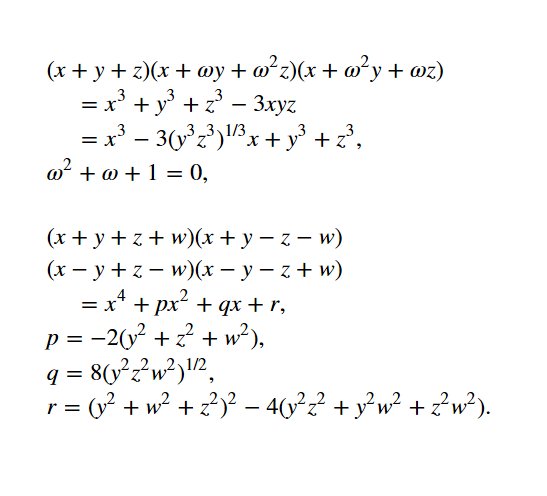
@genkuroki #数学 おとといのE.フレン系さんの白熱教室では algebraic number field についても説明したようですね。数学用語としての field は体と訳されるのですが、フレンケルさんの講義については片仮名英語でフィールドと訳した方が〜続く
@genkuroki #数学 続き〜ニュアンスが伝わりやすい感じもしました。number field を数体と訳すのではなく、「数のフィールド」と訳せば、「数たちが集う場所」のような意味として数学的定義を知らない人達にも伝わるかなと思いました。以下、そういうやり方で説明。続く
@genkuroki #数学 フレンケルさんは有理数たちが集うフィールドに√2を付け加えて新たな数のフィールドが作られるという話をしていました。これは中学生でも本質的に知っていることです。α=√2を有理数のフィールドに付け加えても、加減乗除が自由にできる。続く
@genkuroki #数学 しかも、中学生であっても、√2を含む加減乗除の計算で√2を-√2で置き換えても同じ計算が成立することに気付いてしまう人は多いと思う。ガロアさんもきっとそうだったのでしょう。眠いので続きは後で
@genkuroki #数学 続き。たとえば、1/(1+√2)=-1+√2 の両辺の√2を-√2で置き換えて得られる等式も成立しています。有理数フィールドに√2を付け加えてできるフィールドは√2を-√2で置き換える対称性を持っているわけです。続く
@genkuroki #数学 続き。一般に、a_iたちがフィールドKの数であるとき、方程式x^n+a_1 x^{n-1}+…+a_1 x+a_0=0のすべての解をKに付け加えてできるフィールドLのK上でのすべての対称性の集合をその方程式のガロア群と呼びます。続く
@genkuroki #数学 続き。一般に二次方程式は判別式Dの平方根√Dを-√Dに置き換える対称性を持っています。三次方程式x^3+q+px=0の場合はどうなるでしょうか?q=y^3+z^3, p=-3yzと置くと高校1年の最初に習う見たことのある式が出て来ます。続く
@genkuroki #数学 最近 #掛算 や #輪環 で話題になった x^3+y^3+z^3-3xyz が出て来ます!それが(x+y+z)(x+ωy+ω^2z)(x+ω^2y+ωz)、ω=(-1+i√3)/2と因数分解されることを使えば、三次方程式の解の公式も得られます。続く
@genkuroki #数学 続き。高1の最初で習う特別な三次式の因数分解の公式は実は三次式方程式の解の公式を作るためにもろに役に立つ公式だったわけです。こういうことはガロア理論入門では定番のネタになっており、数学的教養のひとつだと言ってよいと思います。続く
@genkuroki #数学 続き。三次方程式の解の公式を書き下すよりも、x^3+y^3+z^3-3xyz=(x+y+z)(x+ωy+ω^2z)(x+ω^2y+ωz)、ω^2+ω+1=0という綺麗な因数分解の公式をそのまま使った方が対称性がよく見えます。続く
@genkuroki #数学 続き。因数分解の公式の両辺は文字x,y,zを入れ替える操作で不変です。たとえばyとzを交換する互換と、x→y→z→xという巡回置換をしても変化しません。後者の巡回置換を右辺で見れば(y,z)→(ωy,ω^2z)という対称性がみえます。続く
@genkuroki #数学 続き。この結果から、一般の三次方程式のガロア群が「3つの文字の置換全体の集合」=「3次の置換群」になっていることと、その具体的作用がどうなっているかがわかります。高1で習う因数分解の公式はこれだけのパワーを持っているわけ!続く
@genkuroki #数学 続き。約200年前のパリに住んでいたガロア少年は方程式を解くことと方程式の対称性のあいだに深い関係があることを見抜きました。対称性の観点から方程式の構造を記述するというガロア少年のアイデアはその後の数学と物理学を完全に塗り替えることになります。続く
@genkuroki #数学 続き。x^3+y^3+z^3-3xyz=x^3+px+qの左辺の因数分解とy^3,z^3をp,qから二次方程式を解くことによって求められることを使えば一般の三次方程式の解の公式が得られる。別の因数分解の公式を使えば四次方程式も解ける!続く
@genkuroki #数学 四次方程式を解くためには(x+y+z+w)(x+y-z-w)(x-y+z-w)(x-y-z+w)=x^4+px^2+qx+rを使うのが便利。左辺は文字x,y,z,wの置換で不変なので、p,q,rはy,z,wの文字y,z,wの置換で不変な多項式。続く
@genkuroki 続き。y^2,z^2,w^2をp,q,rから求める方程式は三次方程式になります。三次方程式の解き方はすでにわかっているので、四次方程式の解き方もわかるわけです。以上の議論から四次方程式の解の世界の対称性もよく見えます。続く
@genkuroki #数学 続き。四次方程式の4つの解は三次方程式と平方根を用いて求められたy,z,wでα=-y-z-w, β=-y+z+w, γ=y-z+w, δ=y+z-wと表されます。これらはy,z,wのうち2つを-1倍する対称性とy,z,wの置換の対称性を持ちます。続く
@genkuroki #数学 続き。それらの対称性を全部合わせると4つの解のすべての置換を実現できる。これで一般の四次方程式の対称性が4次の置換群になることと、その作用の具体的な様子もわかりました!本質的にすべて高校1年レベルの話です。計算ですべてを確認できる。続く
@genkuroki #掛算 一般のn次方程式にはn個の解を自由に置換するn次の置換群の対称性を持つのですが、3次と4次の場合には特別なことが起こっていることが、以上の高校1年生レベルの計算からわかります。その特別なことのおかげで方程式が解けてしまったわけです。続く
@genkuroki #掛算 一般の三次方程式の3つの解はα=-y-z, β=-ωy-ω^2z, γ=-ω^2y-ωzと書けて(ω^2+ω+1=0)、解達の置換対称性は、(y,z)→(ωy,ω^2z)で生成される位数3の巡回群の対称性とyとzを交換する対称性に分解されている!続く
@genkuroki #数学 すでに解説したように、一般の四次方程式の場合には、4つの解の置換対称性は、3つの文字のうち2つを-1倍する対称性と3つの文字の置換対称性(さらにそれは2つのものの交換対称性と位数3の巡回群の対称性に分解される)に分解されるのでした!続く
#数学 続き。まとめると、一般の4次方程式の4つの解の置換対称性は「3つの文字のうち2つを-1倍する対称性」「2つのモノの交換対称性」「位数3の巡回群」の3種類の対称性に分解されます。これらの対称性は群の言葉で言えばどれも可換群(アーベル群)になっています。続く
#数学 続き。平方根と立方根を含むべき根を取る操作によって数のフィールドを拡大する場合の対称性はアーベル群になります。だから、べき根を取る操作と四則演算だけで解ける方程式の対称性はアーベル群の積み重ねに分解されることがわかります(この辺は総合的には大学3年レベルの話)。続く
#数学 続き。n次方程式がべき根と加減乗除だけで解けるための必要十分条件はその方程式の対称性(ガロア群)がアーベル群の積み重ねになっていること(可解群)になっています。4次以下の方程式は実際にそうなっているので(これは高1レベル)、べき根と加減乗除だけで解けるわけです。続く
#数学 続き。4次以下までは特別に良いこと(4次以下の置換群がアーベル群の積み重ねになっていること)があるので方程式が解けた。しかし、一般の5次以上の方程式ではそういうことが起こらない(5次以上の交代群は単純群)ので、べき根と加減乗除だけで方程式が解けないことがわかります。続く
#数学 続き。以上は11/20(金)に放送されたE.フレンケルさんの数学ミステリー白熱教室への補足。フレンケルさんが説明を省略していた部分を埋めたつもり。方程式の対称性が、アーベル群の積み重ねになっているか、そうなっていないかで、べき根と加減乗除で解けるかどうかが決まります。
#数学 続き。数学の話はお話を聞いただけでピンと来ることはほとんどないと思います。最低でも高校1年レベルの計算をある程度やっておかないと、フレンケルさんが何を言いたいかは理解できないと思いました。数学ネタを一般向けに話すときには色々つらいところがあります。
#数学 続き。4次方程式の計算よりも、3次方程式の計算の方がやさしいので、まずそちらをやっておくべきだと思います。高校1年の最初の頃に習うx^3+y^3+z^3-3xyzの因数分解の公式を使えば一般の3次方程式の解の公式を作れます。返答連鎖をたどれば解説がある。
#数学 YouTubeでここ1週間の「数学ミステリー白熱教室」を検索→ https://www.google.co.jp/search?q=�%95�学ミステリー白熱教室&tbm=vid&tbs=qdr:w …
#数学 続き。本当に面白くて深いのは、一つひとつの方程式を別々に考えるのではなく、「与えられた数体上のすべての代数方程式全体の世界がどうなっているか?」を考えること。数と函数(もしくは幾何)との類似によって「コンパクト・リーマン面の分岐被覆全体の世界はどうなっているか?」を~続く
#数学 続~考えることができます。(コンパクト)リーマン面の(分岐)被覆は位相幾何(トポロジー)の話になるのですが、位相幾何的な被覆の理論は代数函数体(リーマン面上の有理型函数全体のなす体)の拡大の理論と同値になります。この場合には「位相幾何=代数」となる。続く
#数学 続き。たとえば、最近みんな知っているような感じになっている楕円曲線は y^2=(xの3次または4次式) という方程式で定義される曲線のことです。複素数の範囲内でグラフを描けば実2次元の曲面になり、非自明なリーマン面の最も易しい場合にもなっています。続く
#数学 続き。一般にy^2=(xの多項式)という方程式で定義される複素曲線(Riemann面)は楕円曲線の一般化なので超楕円曲線と呼ばれています。y^2=f(x)をyに関して解くy=±√f(x)になり、√f(x)と-√f(x)を交換する対称性があるということになります。続く
#数学 続き。超楕円曲線という名の曲面は見た目の形的にも「√f(x)と-√f(x)を交換する対称性」に対応する対称性を持っていることになります。図を描けるが面倒なので描かない。こういう感じで、数に関する方程式論の直観を曲面の幾何の直観に置き換えることができます。続く
#数学 続き。曲面の位相幾何の立場でガロア理論を理解しておくことは、2次元量子共形場理論とラングランズ・プログラムの関係を理解するためには必須。そういうことを学びたければ久賀道郎著『ガロアの夢』という名著がおすすめ。 http://www.amazon.co.jp/dp/4535781222
#数学 y^2=105 と y^2=x(x-1)(x-2) は似ています。前者は簡単な二次方程式の話ですが、後者は楕円曲線(曲面の幾何)の話になります。この二つは明らかに似ています。
#数学 続き。しかし、個人的な意見では、√2と-√2を交換する対称性は簡単過ぎてガロア理論がどういう世界かをイメージするためには不十分だと思う。2次方程式x^2=aの対称性だけではなく、3次と4次方程式の対称性の様子を見ればイメージがかなり豊かになります。続く
#数学 続き。高校1年生レベルの数学の知識があれば、x^2=aと同様の感覚で3次と4次方程式の対称性を観察することができます。3次方程式の対称性の観察はほとんど「高校1年で習うx^3+y^3+z^3-3xyzの因数分解の公式の話」そのものになっています。続く
#数学 続き。4次方程式の対称性も観察もほぼ同様の感覚で行うことができます。詳しくは以下のツイートから始まる連続ツイートを見て下さい。https://twitter.com/genkuroki/status/668271071729070080 …
#数楽 https://twitter.com/vecchio_ciao/status/691966121411383296 …中1で「錐体の体積を求めるとき、なぜ3で割るのか」と数学の先生に質問したが説明してもらえず、立方体の分割で納得したという話。まず質問の内容も解決方法も滅茶苦茶良すぎ。続く
@genkuroki #数楽 おそらく、「三角形の面積を求めるときになぜ2で割るのか」と同じ方法で「錐体の体積をもとめるときになぜ3で割るのか」について納得したのだと思う。これらは2次元と3次元の場合。n次元では「なぜnで割るのか?」という問題になる。
@genkuroki #数楽 「n次元の錐体の体積を求めるときにになぜnで割るのか」は本質的に「x^{n-1}の積分をするときになぜnで割るのか」(不定積分がx^n/nになる)と同じ話になります。n=2,3の場合を理解していれば一般の場合は「以下同様」!
@genkuroki #数楽 正方形は2つの合同な三角形{(x,y)|0≦x≦y≦a}と{(x,y)|0≦y≦x≦a}の和集合になるので、片方の三角形の面積は正方形の面積の2分の1になります。これを素直に3次元に拡張する方法がわかればn次元まで足をのばせる。
@genkuroki #数楽 立方体は三角錐{(x,y,z)|0≦x≦y≦z≦a}およびx,y,zの大小関係の順番を入れ替えてできる全部で3!=6個の違いに合同な三角錐の和集合になります。だから三角錐の1つの体積は立方体の体積の3!分の1になる。
@genkuroki #数楽 ゆえに全く同様にしてn次元の三角錐{(x_1,…,x_n)|0≦x_1≦…≦x_n≦a}の体積はa^n/n!になります。nそのものじゃなくてnの階乗n!で割っていることに注意。nで割る話との関係は次のツイートで。
@genkuroki #数楽 先のn次元の三角錐の底面{(x_1,…,x_{n-1},0)|0≦x_1≦…≦x_{n-1}≦a}の面積はa^{n-1}/(n-1)!なので、それに高さaをかけるとa^n/(n-1)!なので、さらにnで割ると三角錐の体積になる。これだけの話。
@genkuroki #数楽 大学の線形代数の講義ではR^nのようなn次元空間について習います。世間一般では4次元程度で心が神秘的な世界に飛んでしまう人が多そうですが、大学の講義では何の感動もなく普通な感じでn次元の話をしてしまう人が結構いるはず。
@genkuroki #数楽 昔と違って現代ではインターネットがあるので、大学の講義ではなく、単なる雑談として普通にn次元の話を聞けてしまう時代。そういう環境で育った次の世代がとても楽しみ。
@genkuroki #数楽 自明な誤植の訂正https://twitter.com/genkuroki/status/692508831675473921 …「違いに合同」ではなく、「互いに合同」と書きたかった。
@genkuroki n次元空間で各成分が0以上1以下になるような「立方体」を考えたときに、m次元の物(通常の直方体で言えば、mが0なら頂点、1なら辺、2なら面)の数は2^(n-m)*nCm でいいのでしょうか?
@sekibunnteisuu #数楽 n次元立方体のk次元の面(例えばk=1の場合は辺)の個数は 2^{n-k} binom(n,k) であっています。ここで binom(n,k)=n!/(k!(n-k)!) は二項係数(組み合わせの数)。メンションを外して続く。
@genkuroki #数楽 n次元立方体として、すべての座標の値の絶対値が1以下のR^nの点全体の集合を考えます。原点(0,…,0)はn次元立方体そのものの重心になる。2^n個の頂点は座標として±1だけを並べた点全体になります。0とnの間の次元の辺や面の重心はどうなるか?
@genkuroki #掛算 n次元空間の回転で原点を重心とする立方体をそれ自身に移すようなもの全体の集合は群になる。そのような回転を表わす行列全体は置換行列と対角成分に±1を並べてできる対角行列の積で行列式が1になるもの全体に一致し、それらの個数は2^{n-1}n!になる。
@sekibunnteisuu #数楽 「裏返し有り」だと倍になって、2^n n! 個になります。n個の座標を並べ替えて、±1倍する操作の全体。n=3次元の通常の立方体の「裏返し無し」の回転の個数は2^2×3!=4!になるのですが、群として4次の置換群S_4と同型になります。
@sekibunnteisuu #数楽 3次元の通常の立方体には重心を通る4本の対角線があるですが、立方体を回転させるとちょうどぴったり4本の対角線のすべての置換を作れます(直線の向きは変わってよいことにする)。地道に楽しく24個の置換を回転で全部作る作業をするだけでわかる。
#数楽 https://twitter.com/genkuroki/status/668271071729070080 … 以降の連ツイで解説した4次方程式の対称性(Galois群)と立方体の回転群がS_4であることの関係。(x+y+z+w)(x+y-z-w)(x-y+z-w)(x-y-z+w)=x^4+px^2+qx+r の解は~続く
#数楽 xに関する4次方程式(x+y+z+w)(x+y-z-w)(x-y+z-w)(x-y-z+w)=0の解はy+z+w, y-z-w,-y+z-w,-y-z+wの4つの-1倍です。ちょうどそれらは次のように立方体の対角線と対応付けられます。続く
#数楽 立方体の対角線は、3次元空間の標準基底をe_1,e_2,e_3と書くとき、e_1+e_2+e_3,e_1-e_2-e_3,-e_1+e_2-e_3,-e_1-e_2+e_3で張られる直線になっています。だから(y,z,w)←→(e_1,e_2,e_3)という対応で~続く
#数楽 続き。だから(y,z,w)←→(e_1,e_2,e_3)という対応で、4次方程式の解と立方体の対角線は1対1に対応しているとみなせます。この対応に気付けば立方体の回転が4次方程式の4つの解達の置換を自然に与えていることがわかります。続く
#数楽 続き。しかも4つの解達の置換は次の2つの操作に分解されることもわかる。「y,z,wの置換」と「y,z,wのうち0個または2個を-1倍する操作」。後者の操作は「4つの解達をそのまま動かさない操作または2個ずつに分けてそれぞれのグループで互換する操作」に対応しています。続く
#数楽 続き。こういう話は所謂Galois理論を習うと納得できることが増えるのですが、4次方程式の解の公式を作る場合に方程式の対称性がどのように効いて来ているかを見るだけでも相当に面白い話になっています→https://twitter.com/genkuroki/status/668271071729070080 …
#数楽 4次方程式の解の(加減乗除とべき根だけを使った)公式を作るためには3次方程式の解の公式が必要になります。その話は→ https://twitter.com/genkuroki/status/668189446005649409 …3次方程式の解の公式は高1で習うx^3+y^3+z^3-3xyzの因数分解の話そのもの。
#数楽 高1で習う因数分解と複素数の話を合わせると、公式x^3+y^3+z^3-3xyz=(x+y+z)(x+ωy+ω^2z)(x+ω^2y+ωz),ω=(-1+i√3)/2が得られるので、結果的に3次方程式の解の公式も得られます。続き
#数楽 しかも3つの解y+z,ωy+ω^2z,ω^2y+ωzの-1倍の置換の操作をyとzを交換する操作と(y,z)→(ωy,ω^2z)とy,zを複素平面で120度回転する操作に分解できます。対称性がAbel群の積み重ねになることと解の公式を作れることは同値(Galois)。
#数楽 タルタリア、カルダーノ、フェラーリの時代に現代の高校1年生が行ったら、方程式を解く決闘では負けることがないような気がします。3次方程式を解くために必要な因数分解の公式は習うし、4次方程式への公式の拡張も易しいし、何よりも複素数を自由に使える点が有利だと思う。
#数楽 あ、 https://twitter.com/genkuroki/status/692578708381544448 … でつけるタグを間違って #掛算 にしてしまっていますね。結構よくやってしまう。
@genkuroki #数楽 テレビでE.フレンケルさんの数学ミステリー白熱教室を見た人はすでに知っていると思いますが、有限体の範囲内で楕円曲線を考えても楽しいことが色々わかります。
@genkuroki #数楽 以下pは素数であるとし、F_pはp個の要素を持つ有限体だとします。楕円曲線y^2+y=x^3-x^2の有限体F_pでの解を求めることは、0からp-1までの整数の組(x,y)で両辺をpで割った余りが等しいものを求めるのと同じことです。
@genkuroki #数楽 楕円曲線(の一つ)の定義方程式y^2+y=x^3-x^2の有限体F_pにおけるすべての解を計算して個数を数える様子を見たければリンク先を見てください。http://app.m-cocolog.jp/t/typecast/606783/512682/84064908 …自分でやれば楕円曲線への理解が深まるはず。
@genkuroki #数楽 驚くべきことは、そのようにして計算した有限体F_pでの楕円曲線の点(方程式の解(x,y)を点と呼んだ)の個数が保型形式と呼ばれるとても良い函数の展開の係数として一挙に得られることです(谷山・志村予想!)。
@genkuroki #数楽 楕円曲線y^2+y=x^3-x^2と保型形式q(1-q)^2(1-q^{11})^2(1-q^2)^2(1-q^{22})^2…の対応については↓http://app.m-cocolog.jp/t/typecast/606783/512682/84135089 …http://app.m-cocolog.jp/t/typecast/606783/512682/84143790 …
@genkuroki #数楽 楕円曲線の有限体F_pでの点の個数はp±2√pの間に入ることが知られています。実はこれは素数分布に関するリーマン予想の有限体上の楕円曲線での類似になっています(ハッセの定理)。有限体上での解の個数の分布の仕方は数学的にとても大事な話になっています。
@genkuroki #数楽 有限体F_pでの楕円曲線の点の個数はp±2√pの間に分布するで、全体を2√pで割ると±1の間の分布が得られます。その分布がどうなるかに関する深い予想が佐藤・テイト予想です、現在では証明がつけられています。
@genkuroki #数楽 楕円曲線y^2+y=x^3-x^2の場合に関する佐藤・テイト予想の数値的確認については→ http://app.m-cocolog.jp/t/typecast/606783/512682/84182968 …以上の話を知っていれば、楕円曲線についてはすでにかなり知っていると思ってよいと思います。
@genkuroki #数楽 「楕円曲線」については以上で説明を止めますが、「楕円函数」「保型形式(保型函数)」と「楕円曲線」の関係についても知っていればさらに世界が広がるのですが疲れたのでこの辺でやめます。
@genkuroki #数楽 大雑把に言えば、楕円函数は複素楕円曲線上の函数のことです。保型形式の話をするためには複素楕円曲線の分類の話をしなけらればいけない。保型函数は複素楕円曲線の同型類に複素数を対応させる函数のことです。話が楕円函数より一段深くなっている。
@genkuroki #数楽 以上では、楕円曲線の群構造についても何も触れませんでした。楕円曲線(無限遠点を含める)には自然にアーベル群の構造が入ります。楕円曲線の周辺はあらゆる数学を使って遊べる楽しい公園のようなものです。数学入門のためにはとてもよい公園だと思う。
@genkuroki #数楽 あと「楕円曲線」と「楕円」は異なる曲線だという点にも注意しておいた方が良かったですかね?楕円曲線は平面3次曲線で、楕円は平面2次曲線です。次数が違っていて、楕円曲線の方が楕円よりも複雑な曲線になっています。
@genkuroki #数楽 楕円曲線をy^2=(xの4次式)という形の方程式で定義することもできます。楕円の弧長を高校数学IIIで習う方法を使って積分で表わすとy^2=(xの4次式)型の楕円曲線が自然に出て来ます。
@genkuroki #数楽 円の弧長を積分で書くと曲線y^2=1-x^2と三角函数が出てくるのですが、円ではない楕円の弧長を積分で書くと楕円曲線(楕円ではない) y^2=(1-x^2)(1-k^2 x^2)と楕円函数が出て来ます。その辺の計算は高校数学IIIの範囲内で理解可能。
@genkuroki #数楽 続き。k→0は楕円→円、楕円曲線→円、楕円函数→三角函数の極限になっています。高校で習う三角函数の話は、パラメーターkによって無限にかつ連続的に広がっている楕円函数全体の世界の端っこだけを見ている話になっています。
@genkuroki #数楽 高校生が楕円函数に触れるには http://kansaimath.tenasaku.com/?page_id=1146 の「楕円関数とおもしろい応用」のtogetterとスライドを見るとよいと思います→ http://kansaimath.tenasaku.com/wp/wp-content/uploads/2015/08/ellipticfunction_ver3.pdf …
@genkuroki #数楽https://twitter.com/labidochromis/status/693259541350207488 …その通りです!楕円函数とは楕円積分で定義される多価函数の逆函数のことです。楕円積分で定義される函数の多価性をきちんと分析すると、その逆函数は複素平面上の二重周期函数になる。続く
@genkuroki #数楽 円周の弧長は円周上の積分で書けるのですが、円周を余計に何周か積分すると円周の長さの整数倍の分だけ多価性が出てしまいます。そのおかげで、その逆函数は周期が円周の長さの周期函数になってくれる。これが三角函数です。楕円函数の場合も本質的に同じことです。
@genkuroki #数楽 楕円函数の教科書として竹内端三著『楕圓函數論』は有名。今ならネットで無料で読める。http://kindai.ndl.go.jp/info:ndljp/pid/1063357 …http://homepage2.nifty.com/~y/books/oldbooks.html …
@genkuroki #数楽 続き。複素解析を使う二重周期函数としての楕円函数論については竹内端三本(無料)を読めば良いと思います。複素数体上で使える様々な道具がもっと一般的な状況でも使えるという事情があるので複素数体上での話は知っておいた方が良いです。続く
@genkuroki #数楽 続き。たぶん「楕円曲線」という用語が数学科出身者以外にもポピュラーになった理由は昔からある楕円曲線暗号が普及したからだと思います。そこで使われているのは楕円曲線のアーベル群構造であり、複素解析を使う楕円函数ではありません。続く
@genkuroki #数楽 複素数体上でなくても楕円函数の類似物(楕円曲線の代数函数体の要素)があるので、有限体上の楕円曲線が応用されている場面であっても「楕円函数」という用語を使うことはそう大きな誤りではないと思いますが、竹内端三本を読んだりすると困ることになる(笑)。
@genkuroki #数楽 初心者のうちは楕円曲線とは「3次方程式(x,yの3次式)=0で定義される平面曲線(に無限遠点を追加してもの)」のことだと思っていた方が無難だと思う。暗号への応用で重要なのは群構造。通常、無限遠点が単位元になるようにアーベル群構造を入れます。
@genkuroki #数楽 計算しながらの楕円曲線入門の中に楕円曲線暗号入門が含まれているものに次の文献があります。http://www2.math.kyushu-u.ac.jp/~s-yokoyama/files/2014Yamagata.pdf …横山俊一、計算する立場からの楕円曲線入門、2014、41頁無料で使える数式処理ソフトを使う講義
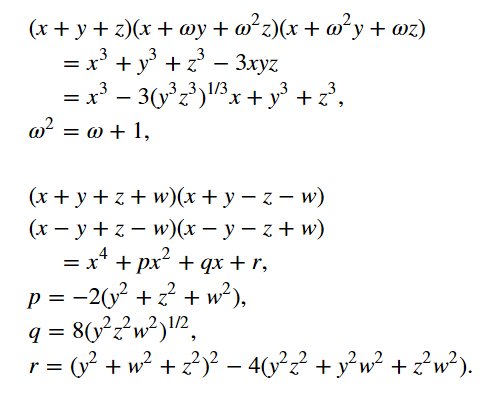
#数楽 "因数分解の公式と3次方程式と4次方程式の解法"https://twitter.com/i/moments/844846853640220673 …
些細な指摘で恐縮ですが、 ω^2 + ω + 1 = 0 かと思います。https://twitter.com/genkuroki/status/844878248131493890 …
さんきゅ。後で直しておきます。