@genkuroki #数学 フレンケルさんの本には日本に滞在していたときの話も書いてあるのだが、フレンケルさんが京大数理研のロビーの前の廊下で師匠のフェイギンさんと空手ごっこをしているのをナマで見たことがある。フェイギンさんが回し蹴りの真似をしていた。
@genkuroki #数学 フェイギンさんとフレンケルさんの写真が https://math.berkeley.edu/~frenkel/Feigin.jpg … にある。その写真へのリンクは http://www.ams.org/distribution/mmj/vol4-3-2004/dedication.html … でのフレンケルさんによる思い出話の最後で見付けた。
@genkuroki #数学 数学ブームというより、もはや「フレンケルブーム」という感じ。今週金曜日夜の最終回にはどんな感想が出て来るか楽しみ。最終回を楽しむためには、第1〜3回目を見逃していても大丈夫だと思う。エドワード・フレンケルさんはそういう喋り方をしています。
@genkuroki #数学 数学ミステリー白熱教室の第3回目でE.フレンケルさんが「3次方程式」と呼んでいるのはより正確には「2変数の3次方程式」。さらに正確に言えば「有理数体上の楕円曲線の方程式」。楕円曲線という専門用語を避けるために3次方程式と呼んでいるのだと思う。
#数学 明日の午後11時からのEテレの数学ミステリー白熱教室(エドワード・フレンケルさん)の最終回を見たい人は忘れずに録画予約を入れておいた方がよいかも。最終回だけを見ても面白いと思います。質問してくれればわかる範囲内で答えることもできます。
#数学 今夜Eテレ11時から、エドワード・フレンケルさんのガチ専門のであるラングランズ・プログラムと理論物理の数学の関係の話があります。フレンケルさん自身の仕事の話なので最も熱い話になるものと予想されます。第1〜3回を見逃していても楽しめると思います。
#数学 エドワード・フレンケルさん、ほんと大人気。説明内容の難易度は過去のテレビ放送の中で最高レベル。それにもかかわらず、大受けしまくっている。NHKは絶対に再放送するべき。放送内容とほぼ同じ話が著書にもある→ http://www.amazon.co.jp/dp/4163902805
@genkuroki #数学エドワード・フレンケル著、青木薫訳、『数学の大統一に挑む』http://www.amazon.co.jp/dp/4163902805 文藝春秋2015/7/13文藝春秋社はいい仕事をしたと思う。この本、ベストセラーにならないかな?
@genkuroki 覚えておられないかもしれませんが、昔、黒木さんの掲示板や表現論の西山亨さんにネット上でお世話になった板垣志朗(しろうくん)です。とねさんの数学&物理系の濃厚ファンサイト紹介…とね日記『数学の大統一に挑む』http://blog.goo.ne.jp/ktonegaw/e/43ca100e56e15427613b009af55c8f7d …
#数学 エドワード・フレンケルさんの数学ミステリー白熱教室がらみの私のツイートは http://twilog.org/genkuroki/hashtags-数学 … でまとめて読めます。一部reply-to連鎖を遡る必要あり。ごめんなさい。2015年11月13日から。
#数学 エドワード・フレンケルさんの話に関連している論文は誰でも無料で読める場所にあります→ http://arxiv.org/ 。個人的にこれはとても素晴らしいことです。さらに個人的な意見を言わせてもらえれば、科学のあらゆる分野で論文を無料公開するべきだと思う。
#数学 たとえば「ウィッテン フレンケル」(Witten Frenkel)をarxivで検索すると→ http://arxiv.org/find/all/1/all:+AND+Witten+Frenkel/0/1/0/all/0/1 …
#数学 昨晩のフレンケルさんの話で主要な例として使われた、SO(3)とSU(2)の定義であれば大学1年生レベルの行列の話を知っていれば理解できます。集合SO(3)の定義は「実3次正方行列Aで、その転置がそれ自身の逆行列になり、行列式が1になるもの全体の集合」です。続く
#数学 続き。集合SU(2)の定義は「複素2次正方行列Aで、その転置の複素共役がそれ自身の逆行列になり、行列式が1になるもの全体の集合」です。どちらも行列の積について群になる。こういう説明の仕方をすると何のことやらわからなくなるので、フレンケルさんの説明の仕方は正解だと思う。続く
#数学 続き。SO(3)のような行列群を直観的に理解するためには、行列が一次変換を表現しているという事実を思い出す必要があります。そして一次変換を直観的に理解している必要があります。一次変換の典型例の一つは「原点を中心とする回転」です。続く
#数学 続き。そういうことがわかっていれば、SO(3)に含まれる3×3の行列は、実3次元空間の回転(を表わす一次変換)と一対一に対応しています。これは3Dゲームプログラミングの基礎。3次元の物体の回転を数学的に表現する方法を知るためにはSO(3)について勉強する必要がある。続く
#数学 続き。SO(3)の定義との関係。実正方行列Aの転置がAの逆行列になるという条件はAが「長さを保つ一意変換であること」の代数的な言い変えになっています。長さを保つ一次変換の中には鏡映変換(x,y,z)→(x,y,-z)も含まれています。これは回転ではありません。続く
#数学 続き。長さを保つ一次変換の全体は実は回転と鏡映変換((x,y,z)→(x,y,-z)以外を含む)で構成されています。そこから回転だけを取り出すための条件が(Aの行列式)=1です。鏡映変換を表現する長さを保つ一次変換を表わす行列は(Aの行列式)=-1を満たしています。続く
#数学 続き。一般に実3×3行列Aの行列式の絶対値をaと書くと、行列Aによる一次変換で体積がa倍になることを計算で確認できます(立方体をAで写した場合にのみを計算すれば十分)。高校レベルの計算で確認できます。行列式と体積の関係は行列式を直観的に理解するために非常に重要です。続く
#数学 続き。問題は行列式の正負が何で決まっているかを直観的に理解すること。行列Aによる一次変換が右手系を右手系に写すとき行列式は正になり、右手系を左手系に写すとき行列式は負になることを示せます。これを理解するのは大学1年レベルだとちょっと手間がかかると思う。続く
#数学 続き。行列と一次変換の関係、転置と内積の関係、内積と長さの関係、行列式と体積の関係、行列式と右手系・左手系の関係、などなどについて健全な直観を十分に身に付けていれば、SO(3)の定義をよく理解できます。健全な直観を身に付けるためには地道に数学の世界を散歩するしかない。続く
#数学 続き。フレンケルさんの話の良かった所は数学の内容そのものにも触れる話もきちんとしていて(寝る聴衆がw)、数学の世界を散歩して健全な直観を地道に身に付けて行けば何が起こっているかがまだ分かっていない数学の世界に近付ける予感が得られるような構成になっていたことだと思います。続
#数学 続き。こういうことを言うと再放送を要求する人が減ってしまうかもしれないのですが、フレンケルさんのような話を聞くことに適正があるのは、「わからないこと」に耐性を持っているだけではなく、「わからないこと」を楽しめる人達の方だと思う。「わからなさ」を楽しめた人は勝ち組!続く
#数学 続き。計算してもわからないものはわからないのですが、計算さえできそうもないことばかりだと「何も見えていない」ということなので、数学の話を聞いたことにはなりません。フレンケルさんの話は難しかったのですが、計算で確認や理解をできる例が多数出て来ました。続く
#数学 続き。最初に出て来た √2 と -√2 を交換する対称性が有理数に√2を付け加えた数の世界(数学者は数のフィールド(number filed、数体)と呼ぶ)に存在することは、中学校レベルで多くの人がすでに体験していることです。ガロア理論はこの話の拡張になっています。続く
#数学 続き。しかし、個人的な意見では、√2と-√2を交換する対称性は簡単過ぎてガロア理論がどういう世界かをイメージするためには不十分だと思う。2次方程式x^2=aの対称性だけではなく、3次と4次方程式の対称性の様子を見ればイメージがかなり豊かになります。続く
#数学 続き。高校1年生レベルの数学の知識があれば、x^2=aと同様の感覚で3次と4次方程式の対称性を観察することができます。3次方程式の対称性の観察はほとんど「高校1年で習うx^3+y^3+z^3-3xyzの因数分解の公式の話」そのものになっています。続く
#数学 続き。4次方程式の対称性も観察もほぼ同様の感覚で行うことができます。詳しくは以下のツイートから始まる連続ツイートを見て下さい。https://twitter.com/genkuroki/status/668271071729070080 …
#数学 続き。フェルマーの最終定理(フェルマー予想)自体は整数に関する予想なのですが、フェルマー予想の多項式版は高校数学レベルで容易に証明できます( http://www.math.tohoku.ac.jp/~ytakao/papers/abc.pdf … )。フレンケルさんの話でも数の世界と函数や幾何の世界の類似が扱われていました。続く
#数学 続き。エドワード・フレンケルさんの研究は、数論由来のラングランズ・プログラムの函数・幾何・理論物理の数学への拡張に関する仕事になっています。だから、数論の話を数の世界限定の話だと思ってしまうとフレンケルさんの話を理解できなくなってしまいます。続く
#数学 続き。数学の世界の異なる場所で同じような法則に支配されているように見える「どうしてそういうことになっているのか」がわかっていない事柄が存在する。この事実を納得できた人はフレンケルさんの話の重要な部分を理解できたと言ってよいと思います。詳細はわかっていなくても。続く
#数学 フレンケルさんの著書の翻訳のタイトル『数学の大統一に挑む』もよく考えて付けられていると思います。原題の"Love and Math"よりも邦題の方が本の内容がよくわかる。 https://www.google.co.jp/search?q=�%95�学の大統一に挑む&ie=utf-8&oe=utf-8&hl=ja …
#数学 続き。フレンケルさんは内容の難解さについて言い訳を色々書いているのですが、「はじめに」のp.19には「この本は数学の知識がなくても理解でいるように書いた」とはっきり書いてあって笑ってしまいました。無理です(笑)。でも、数学の知識がなくても楽しめるように書かれています。
#数学 続き。回転群SO(3)とラングランズ双対SU(2)の解説。SU(2)は複素2次元ベクトルの複素一次変換による回転で行列式が1になるもの全体の集合です。これは図形的には3次元球面(内側は4次元)になります( https://twitter.com/genkuroki/status/671237511474249728 … )。続く
#数学 続き。SU(2)は3次元球面x^2+y^2+u^2+v^2=1の点に対してz=x+iy,w=u+ivとおき(1,1),(2,1),(1,2),(2,2)成分をそれぞれz,w,-(wの複素共役),(zの複素共役)と定めてできる2×2の複素行列全体の集合に等しい。続く
#数学 続き。あ、テキトーに説明し過ぎて大嘘を書いてしまいました。ごめんなさい。長さを保つ実一次変換で行列式が-1のものが鏡映変換になると言ってしまいましたが、単純に誤りです。xy平面の回転とz軸の向きを反転させる鏡映変換の合成は鏡映変換になっていません。アホすぎ。よくある。続く
#数学 続き。回転の行列による取り扱いについては、佐武一郎著『線型代数学』の第IV章がおすすめ。IV§6にSO(n)の連結性の証明が書いてあります。そこを読めばxy平面の回転とz軸反転の鏡映変換の合成は行列式が-1のO(3)の元の典型例になっていることもわかります。続く
#数学 続き。大学1年で習う線形代数の基本は「よい基底を選ぶ方法」です。線形写像の定義域と値域で別々にうまく基底を選ぶことは本質的に連立一次方程式を解くことと同じ(これは簡単)。面白いのは一次変換に相性がよい基底を選ぶ方法です。最も基本的なのは行列の対角化。続く
#数学 続き。固有値が基礎体に含まれなかったり、対角化可能でなかったりすると、単純な行列の対角化のテクニックだけでは足りなくなるのですが、基本的な考え方のほとんどが行列の対角化の話の中に出て来ます。佐武一郎『線型代数学』が数十年前からの定番の教科書。続く
#数学 続き。SU(2)とSO(3)の関係は、フレンケルさんが実演していた「マグカップまわし」でよく説明されます。数十年前からそのように説明されていたと思う。計算でそれを確認するためにはSU(2)に含まれる2×2の複素行列から3次元空間の回転を作り出す方法を知れば十分です。続く
#数学 続き。実3次元空間の点(x,y,z)と2×2行列X=[ ix, -y+iz][y+iz, -ix]を同一視して、SU(2)の行列AによってXをAXA^{-1}に移す変換を考えると実3次元空間の回転が得られます。Pauli行列を考えてもよいです。続く
#数学 SU(2)はα=a+bi+cj+dk, a^2+b^2+c^2+d^2=1 (a,b,c,dは実数)の形の四元数全体の集合とも同一視できるのですが、ξ=xi+yj+zkをαξα^{-1}に移す変換を考えれば3次元の回転が得られます。
#数学 回転の行列による表現はものすごく基本的なことなので、本当はできるだけ早く学んでおいた方が得なのですが、みっちり教わる機会はなかなかないと思います。自分で数学の世界を散歩するときに、「回転の行列による表現」にしばらく滞在するのはよいことだと思います。
#数学 実数θに対してe^{-iθ},e^{iθ}を2つの対角成分とする対角行列AはSU(2)の元です。3つ前のツイートの方法でAから3次元空間の回転を作ると(x,y,z)はx→x, y+iz→e^{2θi}(y+iz)と変換されます。これはyz平面の角度2θの回転です。続く
#数学 続き。行列の掛算についてちょっと知っていれば以上の計算は複素数について知っていれば実行できます。SU(2)内での角度θの回転は3次元空間の角度2θの回転(SO(3)の元)を与えます。これがフレンケルさんが実演していた「コップまわし」の数学的解釈です。続く
#数学 で、フレンケルさんは「ラングランズ双対群」の定義の説明を避けて、最も簡単な場合であるSU(2)とSO(3)を例に挙げるだけですませています。一般の場合については「ルートデータ」という対称性の構造を決める「遺伝子」の話をする必要があります(それ自体が非常に面白い話)。続く
#数学 続き。SU(n)は単連結という「これ以上たくさん被覆できない」という位相的に単純な性質を持っています。そのような単連結なSU(n)のラングランズ双対はそれを中心で割ってできる随伴群になります。SU(n)の随伴群はPSU(n)=SU(n)/{1のn乗根×単位行列}です。続く
#数学 続き。SU(2)とSO(3)=PSU(2)=SU(2)/{±E}は互いにラングランズ双対。より一般の場合にはここまで単純ではなくて、ルートデータの双対でラングランズ双対群を定義します。あと、コンパクト群ではなくて、その複素化を考えた方が便利なことが多い。続く
#数学 続き。SU(2)、PSU(2)の複素化SL(2,C)とPSL(2,C)も互いにラングランズ双対であると言います。この場合の幾何学的ラングランズ対応は、リーマン面上のPSL(2,C)接続にSL(2,C)主束のモジュライ空間上のD加群(線形微分方程式)が対応するという~続く
#数学 続き~話になります。リーマン面上のPSL(2,C)接続は局所的に(d/dz)^2-p(z)のように表示できるのですが、座標変換での貼り合わせはちょうどVIrasoro代数から来るエネルギー運動量テンソルT(z)と本質的に同じになります。続く
#数学 続き。こういう形でリーマン面のガロアサイドがVirasoro代数と結び付くことになります。PSL(2,C)接続(d/dz)^2-p(z)のp(z)の局所的展開の係数からSL(2,C)に付随する共形場理論の仕組みを利用して主束のモジュライ上のD加群を作れる。続く
#数学 続き。その対応が欲しい対応(ヘッケ固有D加群の構成法)になっているというのが、その場合の「幾何学的ラングランズ予想」なのですが、どこまで解決しているかについては知りません。遊ばないといけないので離脱。
#数学 E.フレンケルさんは数学ミステリー白熱教室第3回で楕円曲線y^2+y=x^3-x^2という「いつものあれ」を題材に色々説明していました。計算のアルゴリズムは明瞭。パソコンなどでテレビと同じ結果を再現したければついでに別の深い事実についても確認した方がよいと思います。続く
#数学 いつもの楕円曲線y^2+y=x^3-x^2の素数位数pの有限体での解の個数の表を作るだけで、ヴェイユ予想のリーマン予想の類似部分、谷山・志村・ヴェイユ予想、佐藤・テイト予想の3つの予想の特別な場合をこの特別な場合に数値的に確認できます。続く
#数学 続き。実際の確認の仕方は https://twitter.com/genkuroki/status/671257536218193920 … 以降の連ツイで詳しく説明しておきました。きれいでわかりやすいグラフが描けたら教えて下さい。グラフの情報を拡散します。続く
#数学 続き。佐藤sin^2予想(=佐藤・テイト予想)を佐藤幹夫さんが発見するために必要になったコンピューターによる計算をやった難波完爾さんによる数学史的に貴重な証言を http://www2.tsuda.ac.jp/suukeiken/math/suugakushi/sympo16/16_8nanba.pdf … で読めます(これは非常におすすめ)。続く
#数学 続き。難波完爾さんは楕円曲線y^2=x(x^2+x+1)とη(x)^2 η(5x)^5を例に色々説明しています。E.フレンケルさんが使った「いつものあれ」以外の例を計算してみたい人はこちらもやってみるとよいと思います。
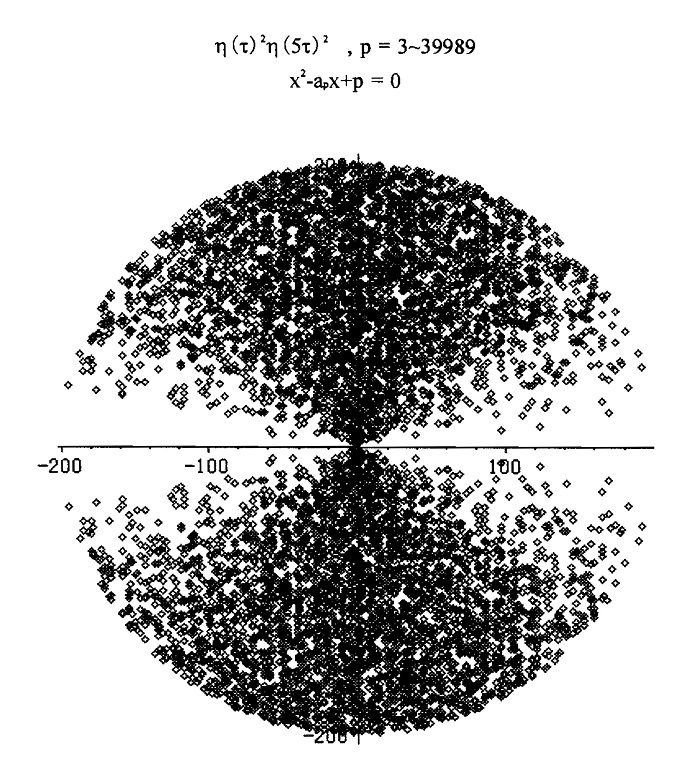
#数学 続き。添付図は http://www2.tsuda.ac.jp/suukeiken/math/suugakushi/sympo16/16_8nanba.pdf … より。複素根をすべてプロット。素数pが4万未満の場合のプロットなので、半径200の円内に入っていることがリーマン予想に類似のハッセの定理の特別な場合。pic.twitter.com/b7iAhf9Hkc

#数学 続き。偏角θで見た分布は(sin θ)^2分布になっていそうな感じ(佐藤・テイト予想が成立している感じ)も根のプロット結果を見ればわかります。 pic.twitter.com/b7iAhf9Hkc
#数学 PSL(2,C)接続(d/dz)^2-p(z)のp(z)dz^2の変換性が共形場理論のT(z)dz^2の変換性と同じなのでガロアサイドのPSL(2,C)接続とVirasoro代数(sl(2)のW代数)が結び付くという話を少し前にしました。続く
#数学 保型サイドの局所版はsl(2)のアフィン・リー環の臨界レベルでの表現論です。sl(2)のW代数は、Virasoro代数であり、臨界レベルではアフィン・リー環の普遍展開環(の完備化)の中心と同一視できます。続く
#数学 さらにsl(2)のW代数は、自由スカラーボソン場を使う実現があります。2つある遮蔽カレントの片方に保型サイドのsl(2)のW代数としてのVirasoro代数が対応しています。もう一方にはラングランズ双対のW代数が対応している。続く
#数学 そして、2つの遮蔽カレントに対応する2つのラングランズ双対W代数(Virasoro代数)は一致することをVirasoro代数の表現論を使うと示せる。臨界レベルの極限で、保型サイドとガロアサイドのVirasoro代数はそれぞれ~続く
#数学 続き~「臨界レベルではアフィン・リー環の普遍展開環(の完備化)の中心」と「PSL(2,C)接続(d/dz)^2-p(z)のp(z)を展開した係数で生成される代数」になります。それらは一致するのでPSL(2,C)接続から臨界レベルの表現が得られるわけです。続く
#数学 続き。局所的な表現が得られれば、後は共形場理論の方法(=アデールを使った保型表現の理論のリーマン面版)を使えば保型表現の類似物が得られます。その表現にはSL(2,C)主束のモジュライ空間上のD加群が対応しており、これが欲しいものだろうというのが私が昔聞いた予想です。つ
#数学 続き。もしかしたら、今現在では非臨界レベルでも1パラメーター族として存在しているW代数のラングランズ双対の物理的もしくは幾何学的理解があるのかもしれませんが、私は現時点では全然知らない。その方面の論文もまじめにチェックしていない。



