#数学 Re:RT みんな、イケメン、イケメン、言い過ぎ(笑)。東洋経済オンラインでもイケメンと→ http://toyokeizai.net/articles/-/92682 … 【イケメン教授のエドワード・フレンケル氏が、「心も頭もしびれる究極の数学」(ツイッターより)を白熱講義するこの番組は〜】
@genkuroki #数学 続き。 http://www.amazon.co.jp/dp/4163902805 の翻訳者までイケメンと言っている→ http://toyokeizai.net/articles/-/92682?page=2 … 【番組が始まってまず思ったのは、「やっぱり、フレンケルってイケメンだわぁ」ということだった】
@genkuroki #数学 個人的な意見では、数学を結構知っていて、かつ、難しい数学の話の高校などでの出前授業の経験もある人であれば、E.フレンケルさんがそんなに上手に話しているようには見えないと思う。本音を言えば私自身もそう感じた。だから結構心配した。続く
@genkuroki #数学 続き。E.フレンケルさんが話した数学的最先端の結果の多くは「確かにそうなることは一応わかったが、どうしてそうなるかはよくわからない」という類の話ばかりなのです。数体、有限体上の曲線、リーマン面、理論物理の場の理論をすべて繋ぐ数学的現象が存在する。続く
@genkuroki #数学 続き。どこで起こっていることも、どうしてそうなるかはよくわからないのですが、複数の世界を比較することによって、少しずつわかるようになって来ている。数論におけるガロアサイドと保型サイドの関係はミステリアスなのですが〜続く
@genkuroki #数学 続き〜、「数体→有限体上の曲線→リーマン面→4次元の物理で2次元の物理を理解すること」という道をたどると、理論物理の世界で主要な研究対象の1つになっている「異なる場の理論のあいだの同値性」で「ガロア・保型対応」が理解できそうだという話になっている。
@genkuroki #数学 そういう話が数学者以外に大規模に宣伝されたのは今回が初めてだと思う。E.フレンケルさんは、ラングランズ・プログラムそのものを解説しようとしたのではなく、ラングランズ・プログラムを1つのネタとして利用して数学の世界の様子を説明しようとしたのです。
@genkuroki #数学 おそらく、数学者内でも、E.フレンケルさんが説明しようとした数学の世界の話を知らなかった人達は多いと思う。複数の数学の分野だけではなく、理論物理の場の理論まで関係しているので、それら全体でどういう世界になっているかを認識することは難しい。
@genkuroki #数学 あと、E.フレンケルさんの話でよかったのは、すごそうに見えるが理解不能な「お話」だけですませることを絶対にしなかったこと。フレンケルさんは地道に誰にでも取り扱える易しい数学的具体例を必ず挿入しようと努力していました。
@genkuroki #数学 あと、フレンケルさんは、実験・観察によって現実の物理とまだ関係がついていない理論物理の結果を利用するときには、実証されていないことにきちんと触れていました。数学の話がメインであっても、そういう点できちんとしているのは、ものすごく印象がよい。
#数学 E.フレンケルさんはクォークと群論の関係を説明していましたが、次のような高校生向けの解説もあります。http://ocw.nagoya-u.jp/index.php?lang=ja&mode=c&id=117&page_type=index …http://ir.nul.nagoya-u.ac.jp/jspui/handle/2237/19424 …林孝宏さんによる2008年度公開講座 : 正多面体と群。
#数学 クォークの話は http://ir.nul.nagoya-u.ac.jp/jspui/handle/2237/19424 … の第2回講義資料 http://ocw.nagoya-u.jp/files/117/tamentai2.pdf … のp.9以降に出て来ます。でも、第1回講義資料から順番に読んだ方が面白いと思う。
#数学 林孝宏さん(よく知っている(^_^))は簡単のためにGL(3)で説明しているのですが、SL(3,C)でも同様で、さらにその極大コンパクト部分群SU(3)に制限しても同様です。E.フレンケルさんは物理学者の流儀にしたがってSU(3)で説明していました。
#数学 数学的なことをまじめに勉強したことがある人であれば、数学的内容は同じなのに記号が違っていたり、同値だが異なるように見える話になっているせいで、理解が困難になる場合が多いことを知っているはずです。そうならずにすむ確率を高めるためには「抽象化」が大事になります。
#数学 実際に目に入る記号操作のパターンに頼り切らずに、背景にある数学的現象そのものに肉薄するような直観的理解をするように努力することが「抽象化」です。正しく抽象的に理解していると、ものすごく具体的な事柄を楽に理解できるようになります。
#数学 SO(3)は(実)3次元空間の回転のさせ方全体の集合とみなせ、SU(2)は3次元空間の回転を2重に持ち上げたものになっていて図形的には3次元の球面(内側は4次元)になっていること、そしてそららは互いにラングランズ双対になっているという事実についてはすでに説明しました。
#数学 さらにU(1)は2次元平面の(原点を中心とする)回転のさせ方全体の集合で、図形的には円周になります。これで、E.フレンケルさんの話に出て来たU(1),SU(2),SO(3)の説明は簡単にしたことになります。残りのSU(3)はクォークを記述する群として登場しました。
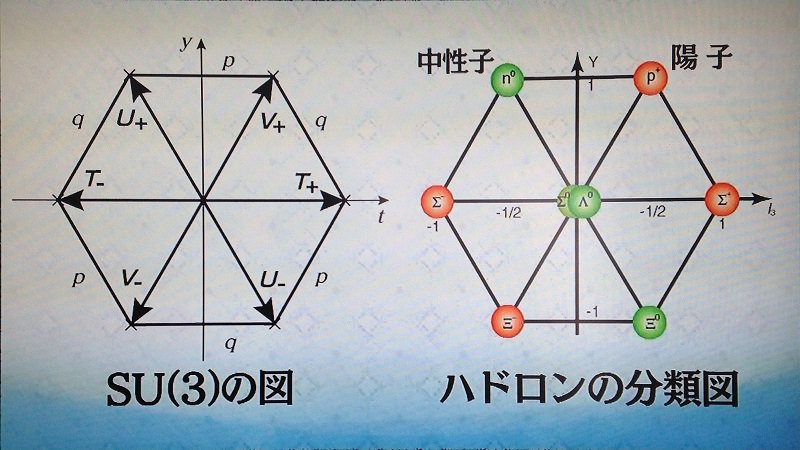
#数学 添付画像は数学ミステリー白熱教室第4回より。図の左半分は「SU(3)のウェイト格子の原点付近の様子」の図になっています。そして右半分は「最高ウェイトΛ_1+Λ_2の8次元既約表現のウェイトたち」の図と同一視できます。続くpic.twitter.com/jzmNL0DJWK
#数学 SU(3)の定義は「複素3次正方行列でその転置の複素共役が自身の逆行列になり、行列式が1であるもの全体の集合」なので、初めて見た人は行列のことを知っていても何のことやらわからないと思います。実は、細かい条件は重要ではなく3×3行列全体を考えてもほぼ同じ話になります。続く
#数学 3次正方行列の全体は3次元の縦ベクトル全体に左から行列の積によって作用しています。第i成分だけが1で他の成分が0の3次元の縦ベクトルをe_iと書くと、e_1, e_2, e_3は3次元の縦ベクトル全体の空間の基底になっています。続く
#数学 続き。物理的にはこのe_1,e_2,e_3が3つのクォークです。3×3行列は3次元の横ベクトルに右から行列の積で作用しています。第i成分だけが1で他の成分が0の3次元横ベクトルをe'_iと書くと、e'_1,e'_2,e'_3は物理的には3つの反クォークだと解釈される。続く
#数学 続き。ただし、横ベクトルには行列が右からの掛算で作用してしまっているので、それを「リー環の左作用」とみなすために、行列を-1倍してから右からの掛算で作用させると約束しておきます。この「-1倍」が反粒子の「反」を意味しています。続く
#数学 続き。以上の説明は行列の掛算について知っているだけで理解できるはずです。今の大学2年生以上は高校のときに行列について習っているので、高校生の時点で知らないうちに3つのクォークの数学的表現と出会っていたと言えます。大学1年生も線形代数の授業ですでに習っている。続く
#数学 続き。さらに、高校や大学で習っていなくても、3Dプログラミングで3×3の行列と3次元の縦もしくは横ベクトルの積を扱ったことがある人達も、知らず知らずのうちに3つのクォークとそれらの反粒子の数学的表現に出会っていたことになります。続く
#数学 続き。数学的な理解は大体においてこんな感じで、身も蓋もないものです。どんなに複雑であっても、細かく分解すれば身も蓋もないほど単純な話になっています。続く
#数学 たとえば、3つのクォークと3つの反クォークが組み合わさって様々な中間子ができる様子は数学的にはe_iたちとe'_iたちの「テンソル積」という名の掛算によって理解できます。3つのe_iと3つのe'_iのテンソル積全体は3×3=9個あります。続く
#数学 続き。それらを基底とする9次元のベクトル空間ができる。その9次元のベクトル空間がリー環の表現として1次元と8次元に既約分解し、その様子がそのまま中間子の記述になっているわけです。続く
#数学 続き。ベクトルとベクトルのテンソル積の数学的定義の仕方は単純なおかげで面白いやり方になっていて、行列の積やベクトルの内積のように何か特別な演算規則によって定義されるのではなく、「(双線形性以外の)演算規則を考えないこと」によって定義されます。続く
#数学 テンソル積a⨂bの扱いは、スカラーαとベクトルa,b,cについて(a+b)⨂c=a⨂c+b⨂c, a⨂(b+c)=a⨂b+a⨂c, (αa)⨂b=α(a⨂b), a⨂(αb)=α(a⨂b)が成立していることを知っていれば十分で、これ以外の関係式を使ってはいけない。
#数学 2つのベクトルを掛算したいと思えばテンソル積によっていつでも掛算できます。そして、テンソル積は「掛算」と呼ぶに値するための必要最小限の条件しかみたしていないと考えるので、テンソル積は他の様々な種類の掛算の「親玉」になっています。専門用語では「普遍性を持つ」という。続く
#数学 ちょっと脱線しましたが、テンソル積のような自明でつまらない事柄でひっかあkるのはアホらしいので、少し説明してみました。数学ではテンソル積のような専門用語が出て来ても、多くの場合、身も蓋もないほど単純な話に過ぎないのでびびらないことが大事。続く
#数学 続き。たとえば2つの文字x,yのテンソル積x⨂yと他の掛算の関係について説明しましょう。文字の積xyは可換性xy=yxを満たしていますが、テンソル積は可換ではありません。しかし、x⨂yをxy=yxに対応させる自然な写像を考えることはできる。続く
#数学 続き。数学ではよく掛算の順序を交換すると-1倍になる積を考えることがあります。文字xとyの外積はx∧y=-y∧x (交代性)を満たす積として定義されます。テンソル積は交代的ではないのですが、x⨂yを外積x∧yを対応させる自然な写像を考えることができます。続く
#数学 続き。脱線しましたが、3つのクォークの複合粒子たちの数学的記述は3つのe_iたちを3つテンソル積たちで記述されます。より詳しくは、3^3=27個のテンソル積から得られる27次元の空間の1次元+8次元+8次元+10次元への既約分解で説明されます。続く
#数学 続き。その8次元の既約成分のうちの片方の基底(8個ある)が数学ミステリー白熱教室で使われた添付図の右半分にある8個のハドロンに対応しています。そしてその図は3×3行列のリー環の8次元既約表現のウェイトダイアグラムとして数学的にはよく知られていたわけです。続く
#数学 続き。3×3行列の話をちょっと拡張(そのちょっとの部分が最初は大変)した話に過ぎないので、その話自体はわかってしまえば身も蓋もないほど単純な話です(テンソル積の既約分解はちょっと複雑)。大学1年生できちんと勉強していれば少し勉強するだけで理解できると思う。続く
#数学 続き。たとえば佐武一郎著『線型代数学』 http://www.amazon.co.jp/dp/4785313013 (古本で買えば安い!この本のコスパ高過ぎ!)の第V章の終わりの「定理(Weyl)」に"3⨂3⨂3"の既約分解の大幅な一般化について書いてあります。続く

#数学 続き。 pic.twitter.com/jzmNL0DJWK 数学ミステリー白熱教室に出て来た添付図をどうやって「身も蓋もない」ほど単純なやり方で描けるのかについて知りたい人もいると思います。完全には説明できませんが、簡単に説明できそうな部分について説明してみましょう。続く
#数学 対角成分が(1,-1,0), (0,1,-1)の3×3の対角行列をそれぞれh_1, h_2と書き、それらを3次元空間中のベクトル(1,-1,0), (0,1,-1)と同一視しておきます。それらの通常の内積は(h_i,h_i)=2, (h_1,h_2)=-1になる。続く
#数学 ベクトルα_iとΛ_iをα_i=h_i, Λ_1=(2,-1,-1)/3, Λ_2=(1,1,-2)/3 と定める。(3×3行列ではなくn×n行列の場合にはΛ_i=(n-i,…,n-i,-i,…,-i)/n (n-iはi個)とおきます。)続く
#数学 続き。このとき内積(h_i,Λ_j)はi=jのとき1、i≠jのとき0になります。さらに、α_1=2Λ_1-Λ_2, α_2=2Λ_2-Λ_1も成立しています。以上は地道に紙の上で計算してチェックして下さい。内積の計算は本質的に高校レベル(対応する成分の積の和)。続く
#数学 続き。少し前に第j成分だけが1で他の成分が0の3次元縦ベクトルをe_jと書いてましたが、ある理由があってこれ以後はv_jを書くことにします。ベクトルv_jたちに行列としてのh_iを作用させた結果を計算しましょう。続く
#数学 続き。結果はh_i v_1=(h_i, Λ_1)v_1,h_i v_2=(h_i, -Λ_1+Λ_2)v_2, h_i v_3=(h_i, -Λ_2)v_3とまとめられます。これも地道に計算すればチェックできます。続く
#数学 続き。一般に「h_i u= (h_i,λ)u」が成立しているとき、「uはウェイトλを持つ」と言います。1つ前のツイートの結果は、v_1,v_2,v_3のそれぞれがウェイトΛ_1,-Λ_1+Λ_2,-Λ_2を持つと言い変えられます。続く
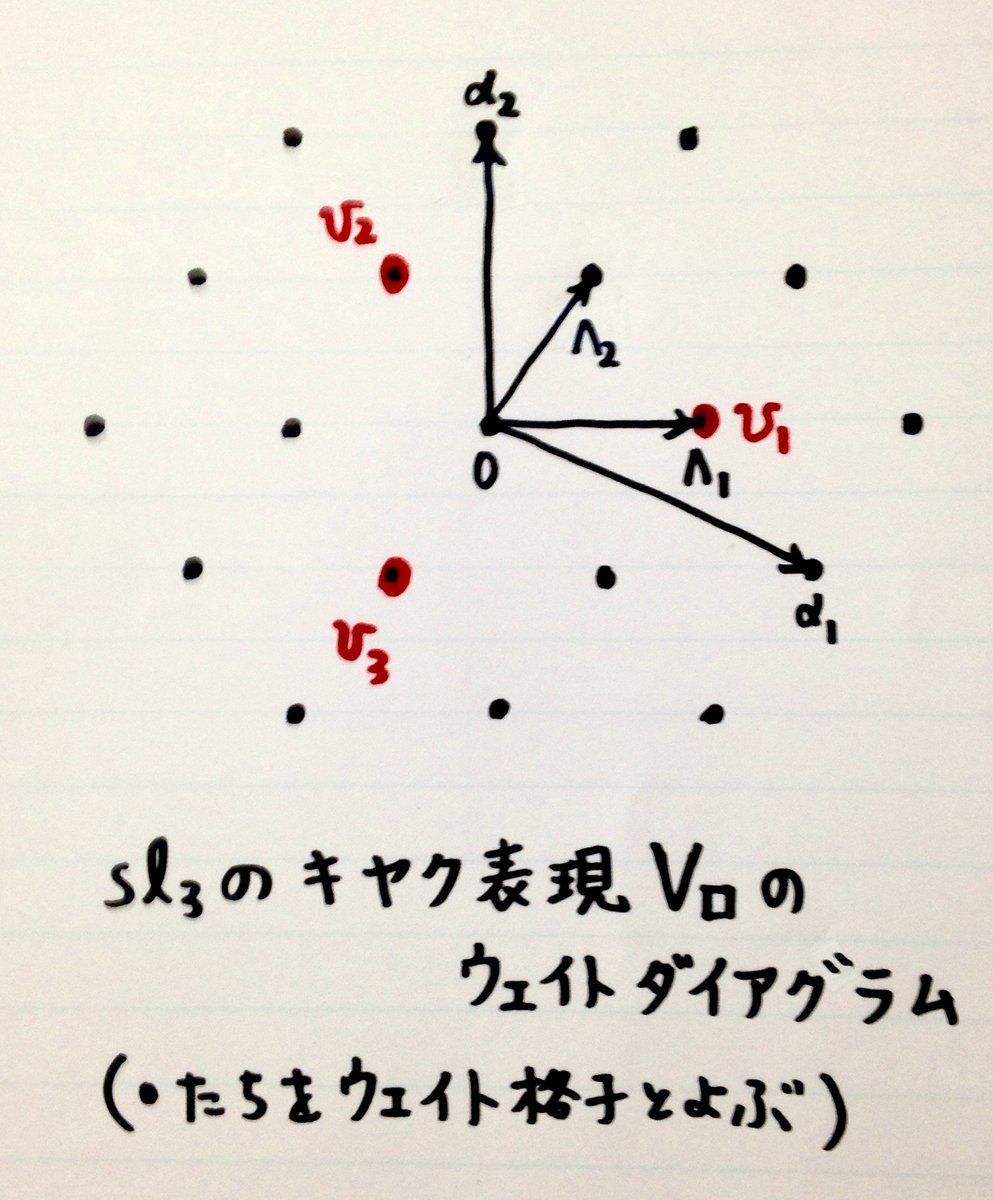
#数学 続き。ベクトルのウェイトたちを平面にプロットしたものをウェイトダイアグラムと呼びます。3×3行列が3次元の縦ベクトルの空間に作用しているケースでのウェイトダイアグラムは添付画像のようになる。pic.twitter.com/xwKb5DHybl
#数学 続き。Λ_iの整数倍たちの和全体の集合をウェイト格子(ウェイトラティス)と呼びます。我々が扱っているケースでのウェイト格子は正三角形がたくさん並んでいるような図になります。続く
#数学 表現のテンソル積の既約分解の説明はしんどいのでしません。ごめんなさい。目標とする8次元表現は直接的には以下のようにして作れます。(i,j)成分だけが1で他の成分が0の3×3行列をE_{i,j}と書き、e_i=E_{i,i+1}, f_i=E_{i+1,i}とおく。続く
#数学 続き。ベクトルwに関する関係式 e_i w=0, h_i w=(h_i,Λ_1+Λ_2)w, f_i^2 w=0 (i=1,2)を仮定します。すると w に f_1, f_2 任意有限回かけて得られるベクトルたち全体で8次元のベクトル空間ができることを確認できます。続く
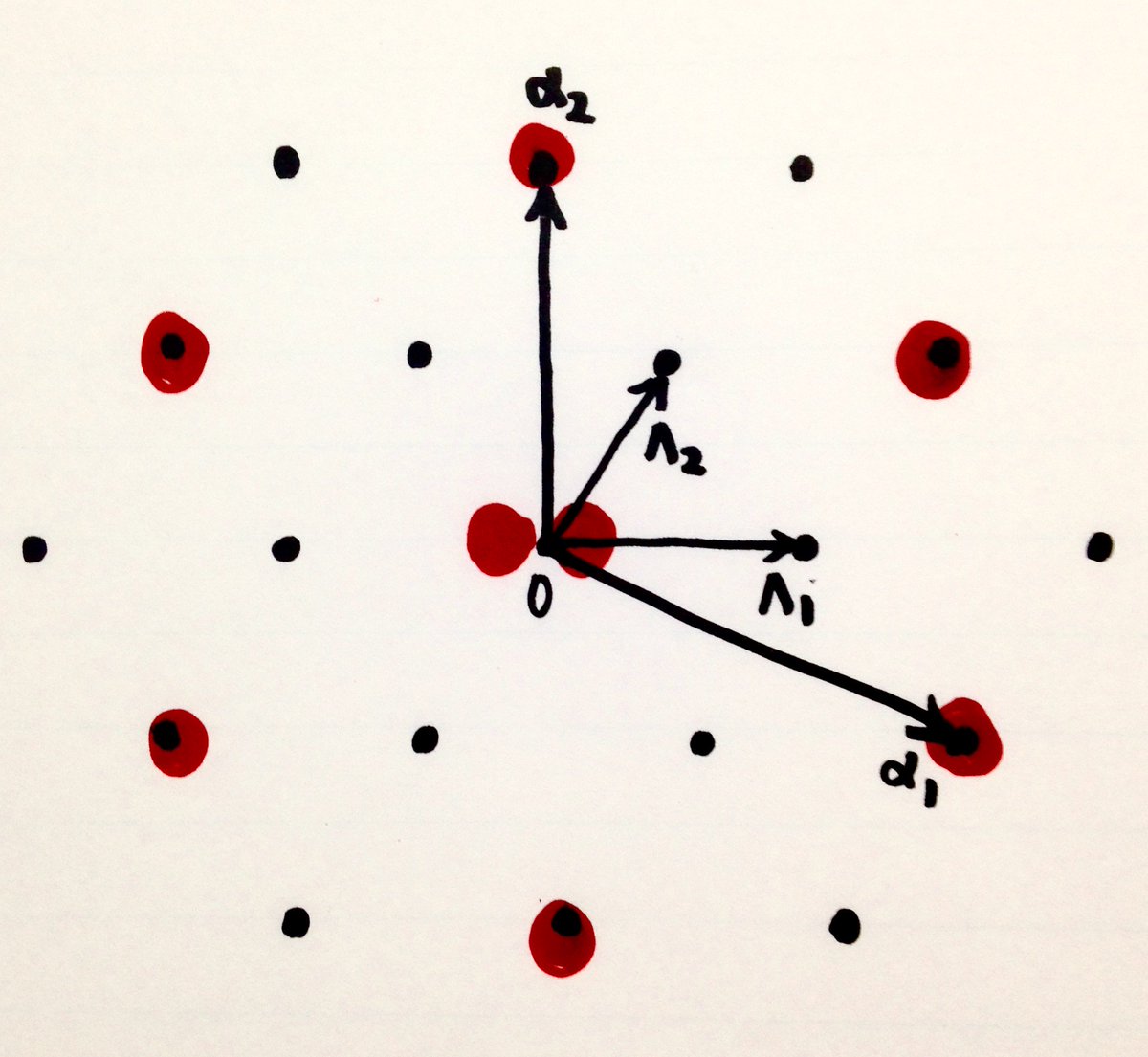
#数学 続き。そしてウエイトたちは8つになり(そのうちの2つは0)、ウェイトダイアグラムは添付画像のようになることを確認できます。これが数学ミステリー白熱教室で出て来た図と本質的に同じものです。pic.twitter.com/fqizYbKLbf
#数学 表現の作り方の別の方法。天下り的ですが、変数x_1,x_2,x_3で生成される多項式環を考え、x_iに関する偏微分を∂_iと書きます。多項式環にh_i,e_i,f_iたちをh_1→-2x_1∂_1+x_2∂_2-x_3∂_3+λ_1,続く
#数学 続きh_2→x_1∂_1-2x_2∂_2-x_3∂_3+λ_2,e_1→∂_1,e_2→∂_2+x_1∂_3,f_1→-x_1^2∂_1-x_1x_3∂_3-x_3∂_2+x_1x_2∂_2+λ_1x_1,f_2→x_3∂_1-x_2^2∂_2+λ_2x_2.
#数学 続き。多項式環の元1にこのようにしてh_i,e_i,f_iたち(実はf_iたちだけで十分)をどんどん作用させていくとリー環sl_3の最高ウェイトλ_1Λ_1+λ_2Λ_2の既約表現が得られます。λ_1=λ_2の場合には8次元の既約表現が得られます。続く
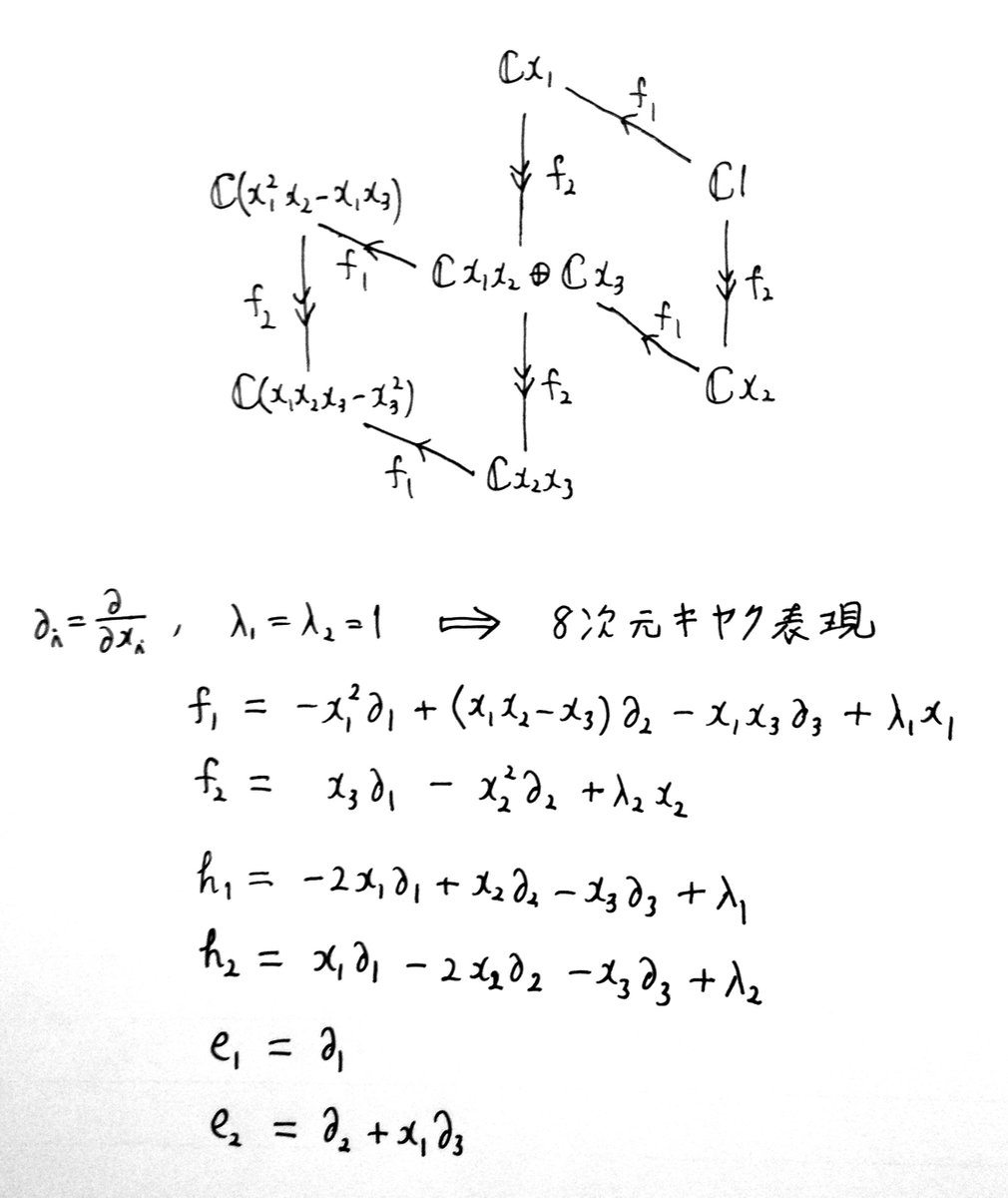
#数学 続き。添付画像は以上の方法による8次元既約表現の計算結果とウェイト・ダイアグラム。(1に微分作用素を作用させる計算をするだけ)pic.twitter.com/YLs2QX192M
#数学 実は以上の計算はE.フレンケル著『数学の大統一に挑む』 http://www.amazon.co.jp/dp/4163902805 のpp.223-224の【旗多様体はたしかにうまくいきそうだった~「ユウレーカ」】の部分の3×3行列の場合(sl_3の場合)の話になっています。続く
#数学 h_i,e_i,f_iたちの微分作用素による表示は実は旗多様体へのリー環の無限小作用をオープンセル上で具体的に書き下したものです。計算のアルゴリズムを知っていれば誰にでも機械的に計算できる類のものです。旗多様体はリー環の表現論で基本的な役割を果たしています。
#数学 答えを知っていれば偏微分の計算法を知っているだけですべてを紙の上の計算で確認できるはずです。こういう類の計算をおそらくE.フレンケルさんも実際にやっていたと思う。そしてそういう計算の例は偏微分の計算さえできれば誰にでも手が届く所にあるということです。
#数学 数学っぽい話を聞くときには、「自分には永久に手が届かないことをやっている」と感じていたら、どこかで間違った道に入り込んでしまったと思う方がよいと思う。実際には身も蓋もない単純だが地道な議論の先で「手が届きそうもないように感じられること」に手が届くようになっているのです。
#数学 拡散! https://twitter.com/genkuroki/status/671257536218193920 … のy^2+y=x^3-x^2関連情報→ http://sci.tea-nifty.com/blog/2015/12/scratchy2yx3-x2.html … 素数pを法とする解の個数のScratchでの計算→ https://scratch.mit.edu/projects/90340774/ …
#数学 続き。素数pに対する解の個数は大体pになります。解の個数とpの差は2√p未満になるというのがハッセの定理。ハッセの定理はリーマン予想の有限体上での楕円曲線での類似になっています。こういうことからも一般化されたリーマン予想の世界が見えます。

#数学 続き https://scratch.mit.edu/projects/90340774/ … y^2+y=x^3-x^2の素数pを法とする解の個数をp=59で計算させてみた。時間がかかりましたが、結構楽しかった。pic.twitter.com/eAcKEUa3Gz
@genkuroki #数学 https://twitter.com/genkuroki/status/673387117477675008 … あたりから書いたことはSU(3)の場合の ラングランズ双対群の説明に繋げる予定だったのを忘れていた。用語:h_iたちは単純子ルート、Λ_iたちは基本ウェイトと呼ばれています。続く
@genkuroki #数学 続き。α_iたちは単純ルートと呼ばれています。SU(3)では単純コルートと単純ルートは一致していますが、一般には一致していません(α_i=2h_i/(h_i,h_i))。単純コルートの整数倍たちの和全体の集合はコルート格子と呼ばれています。続く
@genkuroki #数学 続き。基本ウェイトの整数倍の和全体の集合はウェイト格子と呼ばれています。さらに基本ウェイトの0以上の整数倍たちの和をドミナント整ウェイトと呼びます。そして、ドミナント整ウェイトの全体と既訳表現というものの全体が一対一に対応している。続く
@genkuroki #数学 続き。ただし、すべてのドミナント整ウェイトに対応する既訳表現が存在するのはSU(3)が単連結だからです。逆にすべてのドミナント整ウェイトの対応する既訳表現を持つ群は単連結になります。既訳表現がたくさんあればあるほど短連結に近づく。続く
@genkuroki #数学 対称性は群で記述されるのですが、SU(3)などの群たちは、すべての単純コルートたちを含む格子とその双対格子ですべての単純ルートたちを含むものの組(ルートデータ)と一対一に対応しています。ルートデータはゲージ対称性の遺伝子の役割をはたしています。続く
@genkuroki #数学 与えられたルートデータの単純コルートと単純ルートを交換し、それらを含む格子たちも交換してものも、ルートデータになっており、双対ルートデータと呼ばれています。双対ルートデータに対応する群がラングランズ双対群の定義です。続く
@genkuroki #数学 先のSU(3)のルートデータはコルート格子とウェイト格子の組になります。単純コルートと単純ルートは等しいので、コルート格子とウェイト格子を交換したものが双対ルートデータになり、それに対応する群がSU(3)のラングランズ双対群になります。続く
@genkuroki #数学 SU(3)の双対ルートデータでは、単純ルートを含む格子がウェイト格子からルート格子というすべて単純ルートを含む最小の格子に縮小されてしまいます。それに応じて、ラングランズ双対群の既訳表現も最小限に減ることになります。続く
@genkuroki #数学 続く。SU(3)のラングランズ双対群はSU(3)と同じ型を持つ(同じ単純コルートと単純ルートを持つ)群でもっとも単連結でないものになります。それはSU(3)/{E,ωE,ω^2E} (ωは1の原始3乗根)になります。一般の場合も同様です。
@genkuroki #数学 SU(2)の単純コルート=単純ルートは1つだけで√2と同一視できます。基本ウェイトは1/√2と同一視できます。コルート格子=ルート格子は√2の整数倍全体の集合になり、ウェイト格子は1/√2の整数倍全体の集合になります。続く
@genkuroki #数学 0以上の整数mに対するドミナント整ウェイトm/√2にはm+1次元の既訳表現が対応しています。ラングランズ双対ではm/√2がルート格子に入る、すなわち√2の整数倍になることが要請されるので、mとして偶数のみが許され、既訳表現は奇数次元になります。
@genkuroki #数学 SU(2)のラングランズ双対のSO(3)は奇数次元の既訳表現しか持ちません。電子のスピンは2次元の既訳表現で記述されるので、SO(3)では電子のスピンを取り扱えず、SU(2)が必要になるわけです。
@genkuroki #数学 ウィッテンさんの自慢の1つは「ガロア・保型対応」でラングランズ双対群が出て来る理由を理論物理の言葉で理解したことだと思います。おそらくそういう理由で、E.フレンケルさんは、一般向けの話の中にラングランズ双対群の話を持ち出したのだと思う。
@genkuroki #数学ウィッテンさんへのインタビューhttp://www2.yukawa.kyoto-u.ac.jp/~tohru.eguchi/articles.html …1990と1994http://www.ipmu.jp/webfm_send/1084 2014後者のp.54(全16頁中11頁目)からラングランズ対応の話が始まります。
@genkuroki #数学http://www.maths.ed.ac.uk/~jmf/Teaching/Lectures/EDC.pdf …Electromagnetic Duality for Children
#数学 ぼくが一番好きなWikipediahttps://en.wikipedia.org/wiki/Dynkin_diagram …Dynkin diagramそこにある大量の図の一つひとつがSU(2)のような群の一般化の「型」を記述している(無限次元版を含む)。続く
#数学 「ディンキン図形(の一般化)」は「単純コルートと単純ルートのあいだの内積表」と一対一に対応している。ディンキン図形は対称性の型を記述しており、SU(2)とSO(3)は同じ型(A_1型)の対称性。ラングランズ双対はディンキン図形の矢線の向きを逆転させる。
#数学 大学1年では行列と行列式について習う。行列式の話では置換群を扱う。対称性の型を記述するディンキン図形の立場で大学1年生で習う線形代数は「A_{n-1}型の線形代数」だとみなすことができる。行列式はまさにA_{n-1}型の対称性から出て来る数学的対象である。続く
#数学 続き。「A型の線形代数」=「普通の線形代数」なのだが、他にも「古典型の線形代数」として「B型、C型、D型の線形代数」もある。B型、D型はSO(n)、C型はSp(n)です。他にもE_{6,7,8}, F_4, G_2の5つの例外型がある。
#数学 http://member.ipmu.jp/yuji.tachikawa/stringsmirrors/2006/witten.pdf …Edward Wittem, Gauge theory and geometric Langlands, 2006, Beijing
#数学 ちょっと別の話。代数体、有限体上の曲線、複素数体上のリーマン面の類似はよく知られているが、リーマン面ではなく、3次元多様体を考えるべきだという話もある。代数体や有限体上の曲線では、各点がまるで閉じた紐のような構造を持っている感じになっています(フロベニウス)。続く
#数学 続き。だから、代数体や有限体上の曲線の話の正しい類似は、「リーマン面とそれ上の点」ではなく、「3次元多様体とその中の結び目」だと言われています。数論的な点の幾何的類似物は結び目だろうと言われています。フロベニウスの幾何的類似は結び目の基本群の作用。
#数学 http://arxiv.org/abs/math/9809057 …On the Lego-Teichmuller gameBojko Bakalov, Alexander Kirillov1998
#数学 https://www.youtube.com/watch?v=V1S_xgfN-d0 …Edward Frenkel and Chris Carter: Love, Mathematics and The X-Files Xファイルとエドワード・フレンケルさん!Xファイルかよ!
#数学 http://www5a.biglobe.ne.jp/~y-toku-i/report/report0.html …徳田裕也、3次元多様体のWitten不変量の2次元共形場理論からのアプローチについて、修士論文(dviファイルのみ)dviファイルの閲覧もしくはpdfへの変換で最も楽な環境の整え方は何だろうか?
#数学 https://www.youtube.com/user/edfrenkel/videos …YouTube Edward Frenkel Ch.https://www.youtube.com/results?search_query=Edward+Frenkel …YouTubeでEdward Frenkelを検索突き抜けている感じで好感が持てる。中途半端じゃない。
#数学 『NHK 数学ミステリー白熱教室 ラングランズプログラムへの招待』黒木玄さんのツイートを主に適当にまとめ - 相転移プロダクション相転移プロダクション http://phasetr.com/blog/2015/12/06/『nhk-数学ミステリー白熱教室-ラングランズプログ-4/ …



