お金の分布としての指数分布とガンマ分布(続き)
#数楽 リンク先の単にランダムにお金をやりとりするだけの世界の話について補足。続くhttps://twitter.com/genkuroki/status/845123663900786691 …
#数楽 人数Nは大きいとし、お金の総量MをNで割った値a=M/N>0はNによらないと仮定しておきます。各人の保有するお金m_iの総和がMになるという条件の下で等確率条件を仮定(ランダムにお金のやりとりをしていると仮定)すると〜続く
#数楽 続き〜、各人の保有するお金がmになる確率は近似的にe^{-m/a}に比例するようになります。すなわち、各人が保有するお金の量が指数分布に近似的に従うようになります。これは数学的には統計力学におけるカノニカル分布の特別な場合とみなせます。続く
#数楽 統計力学におけるカノニカル分布を体験してもらうために、おもちゃのお金を配ってランダムにお金をやりとりさせると、指数分布が現れることを確認する授業をやっている人もいるらしいです。(本当の話をするとよく知りません。)続く
#数楽 指数分布はあまりにも不平等なので、なんとか平等に近付けたいと仮に思ったとしましょう。そのためには、ある種の効用の総和に下限を設けるという手段が(数学的には)使えます。お金mから得られる各人の効用はlog mだと仮定しましょう。続く
#数楽 続き。logは上に凸な単調増加函数の例としてよく使われます。相加相乗平均の不等式もしくはJensenの不等式より、各人の効用log m_iの平均値はlog a以下になります(aはm_iの平均値でした)。効用log m_iの平均値がlog aになるのは〜続く
#数楽 続き〜、全ての人が持つお金が等しくaになる完全平等状態です。そこまで極端ではなく、0<b<aであるとし、「効用log m_iの平均値はlog b以上である」という制限の下でランダムにお金やりとりをさせたらどうなるでしょうか?m_iの平均値はaで一定であるとします。続く
#数楽 続き。そのとき各人の保有するお金がmになる確率は近似的にexp(-m/μ+(λ-1)log m)に比例するようになります。すなわち近似的にガンマ分布に従うようになる。μとλはaとbからλμ=a,log μ+Γ'(λ)/Γ(λ)=log bで決まります。
#数楽 続き∫_0^∞ e^{-x/μ}x^{λ-1}dx=Γ(λ)μ^λ(1/Γ(λ)μ^λ)∫_0^∞ e^{-x/μ}x^{λ-1}x dx=λμ(1/Γ(λ)μ^λ)∫_0^∞ e^{-x/μ}x^{λ-1}log x dx=log μ+Γ'(λ)/Γ(λ)
#数楽 続き。すなわち、λμ=a、log μ+Γ'(λ)/Γ(λ)=log bはガンマ分布する確率変数X(今の場合は各人が保有するお金の量)について、(Xの平均)=a(log Xの平均)=log bを意味しています。続く
#数楽 続き。b_0(a)をlog a+Γ'(1)=log b_0(a)、Γ'(1)=-γ=-0.5772…と定め、以下b_0(a)≦b≦aと仮定します。人数をNとする。お金の総量をΣm_i=Naとし、効用の総和をΣ log m_i≧N log b と~続く
#数楽 続き~制限して、ランダムにお金をやりとりしまくると、各人が保有するお金の量はa,bから定めたパラメータλ≧1,μ>0に関するΓ分布に近似的に従い、指数分布より「平等」な状態が確率的に実現されます。
#数楽 今のケースでは統計力学での逆温度にあたるパラメータが2つあって、1/μ>0と1-λ≦0の2つが逆温度にあたるパラメータです。後者が負になっていることに注意。
#数楽 逆温度にあたるパラメータβが負になるケースも含めた議論が私のノートに書いてあります→ http://www.math.tohoku.ac.jp/~kuroki/LaTeX/20160616KullbackLeibler.pdf … (特に第4節)
#数楽 問題:等確率の原理が崩されないようなランダムにお金をやりとりするルールで、「お金の総量がNaで一定」と「log型効用の総和がN log b以上」という条件を満たす扱いやすいもの(教室内の実験で使えるもの)を見つけよ。
#数楽 この問題が解ければ、log型効用の総和に下限を設ければ、自然に指数分布より平等なガンマ分布が確率的に勝手に実現してしまうという実験が教室内でできます。
#数楽 お金の総量一定でランダムにお金をやりとりすると、個人保有のお金の量の分布が指数分布に近付く統計的な力が働きます(条件付き大数の法則)。効用の総和に下限を設けるとによって指数分布に近付くことを妨げると指数分布とは異なる分布に近付くことになります。これはそういう話。
#数楽 この辺のことは相対エントロピー(Kullback-Leibler情報量)に関するSanovの定理がどういう結果であるかを直観的に理解すれば、当たり前の話に感じるようになります。
#数楽 上の方で出て来たγ=-Γ'(1)=0.5772…は所謂オイラー定数です。円周率や自然対数の底の次くらいによく出て来る感じ。この手のことに慣れていない人はWolframAlphaに慣れると良いと思います。便利だし、勉強になります。
#数楽 あとΓ(s)=∫_0^∞ e^{-x}x^{s-1}dxはガンマ函数。ベータ函数とともに、指数函数、対数函数、三角函数の次くらいによく出て来る。高校で教えた方がいいんじゃないかと思えるくらい、数学を使うとよく出て来ます。知らないと統計がらみの話はついて行けなくなる。
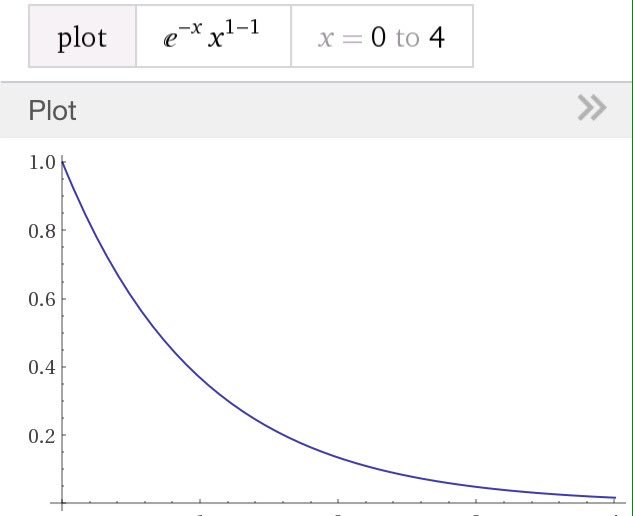
#数楽 添付画像は平均1の指数分布のグラフです。λ=1/μ=1の場合。正規化していないので、縦軸の目盛りは無視来てください。保有するお金の量が小さいほど確率が高くなる。現実の貯金の分布もこんな感じ。pic.twitter.com/D9p1DJeerG
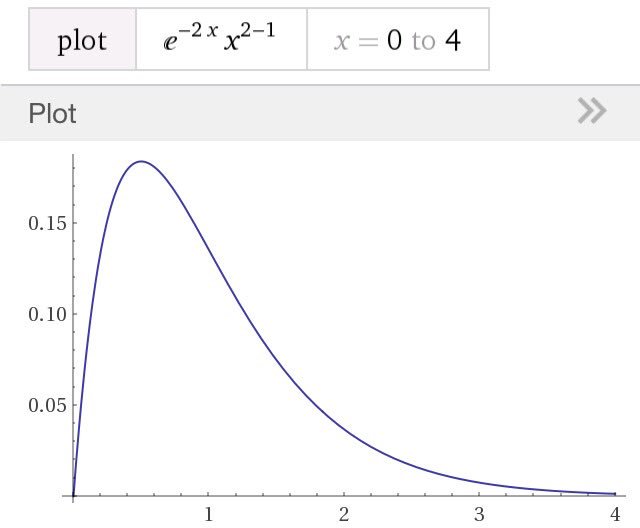
#数楽 平均は1のままだが、λ=2としたガンマ分布のグラフ。λ=1/μ=2の場合。お金を全然持っていない人が減っている。縦軸の目盛りは無視してください。pic.twitter.com/iR5mmUrNMp
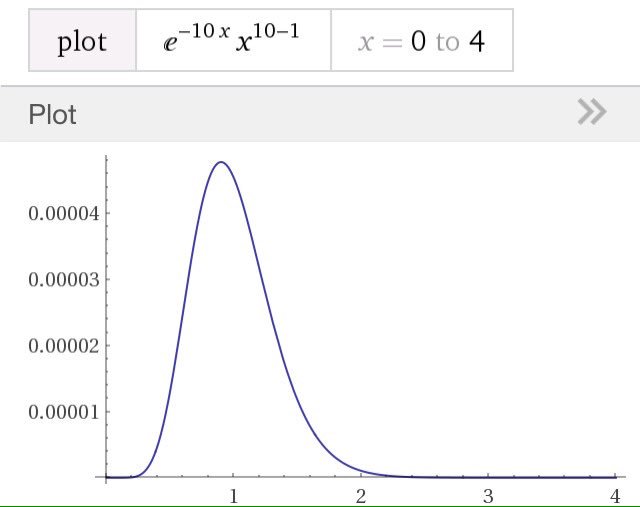
#数楽 リンク先の「統計的な力」の自明な例は大数の法則です。たとえば、表と裏が同じ確率で出るコインを投げ続けたら、出た表の数と裏の数の比は1対1に近付きます。まるで表の数と裏の数の比が等しくなる力が働いているように錯覚できる。続くhttps://twitter.com/genkuroki/status/845842129310048258 …
#数楽 続き。もっと複雑な分布の場合でも同様に自明な(大数の法則による)「統計的な力」が働いていると思うことができます。たとえば1からrまでの目がそれぞれq_1,…,q_rで出るルーレットを何度も回し続ければ、1からrまでの目が出た数の比はq_1:…:q_rに近付きます。続く
#数楽 続き。以上のような単純な大数の法則による「統計的な力」は確率の概念を正しく理解している人にとっては自明過ぎてつまらないと感じられると思う。非自明で面白いのは「条件付き大数の法則」です。続く
#数楽 続き。たとえば、自由にお金をランダムにやりとりするとお金の分布が指数分布になる状況に「効用の総和がある定められた下限以上になる」という条件を課して確率分布をガンマ分布に変えるというようなことができるわけです。こちらの話は非自明で面白い話だと思います。
#数楽 一般に以下が成立しています。まず、制限抜きの確率分布(確率密度函数)はq(x)だとします。何の制限も付けないと乱数xが分布q(x)に従って生成される。次に、f(x)はxの任意の函数であり、分布q(x)に関するf(x)の平均をc_0と書きましょう。続く
#数楽 続き。c<c_0 のとき、分布q(x)に従って、N回乱数x_1,…,x_Nを発生させ、(f(x_1)+…+f(x_N))/N≦cが成立する場合以外を全て捨て去ると、Nが大きいとき~続く
#数楽 続き~、そのように制限された乱数列x_1,…,x_Nはまるで確率分布p_β(x)=e^{-βf(x)}q(x)/Z(β)に近似的に従っているかのように振る舞います!ここで、Z(β)=∫e^{-βf(x)}q(x)dx、⌠f(x)p_β(x)dx=cです。続く
#数楽 続きc>c_0の場合には、分布q(x)に従ってN回乱数x_1,…,x_Nを発生させ、(f(x_1)+…+f(x_N))/N≧cが成立する場合以外を全て捨て去ると、Nが大きいとき~続く
#数楽 続き~、そのように制限された乱数列x_1,…,x_Nはまるで確率分布p_β(x)=e^{-βf(x)}q(x)/Z(β)に近似的に従っているかのように振る舞います!ここで、Z(β)=∫e^{-βf(x)}q(x)dx、⌠f(x)p_β(x)dx=cです(βは負になる)。
#数楽 続き。c<c_0のときβは正になり(この場合が統計力学に出て来る)、c>c_0のときβは負になります(βが負の場合を扱った説明が確率論の文献によくあります)。逆温度βは負になっても全然問題ない。
#数楽 例えば、q(x)=e^{-x/a}/a (a>0、指数分布)のケースで、f(x)=log xのとき、c_0=(1/a)⌠_0^∞ e^{-x/a} log x dx=log a-γ (γはオイラー定数)であり、c=log b<log a-γと仮定すると、続く
#数楽 続き、q(x)が生成する乱数x_1,…,x_Nを(log x_1+…+log x_N)/N≧c=log bの場合に制限すると、x_1,…,x_Nは分布p_β(x)=e^{-β log x}e^{-x/a}/Z(β)に近似的に従っているかのように振る舞います。続く
#数楽 続き。ここでZ(β)=∫_0^∞ e^{-β log x}e^{-x/a} dx=∫_0^∞ e^{-x/a}x^{-β} dx=Γ(1-β)a^{1-β}であり、⌠_0^∞ p_β(x) log x dx=c=log bでβを決めます。βは負になる。続く
#数楽 現在 http://math.tohoku.ac.jp/~kuroki/LaTeX/ にアクセスできなくなっています。最近ずっと使いまわしている解説のコピーを以下の場所に置いておきました。http://genkuroki.web.fc2.com/20160501StirlingFormula.pdf …http://genkuroki.web.fc2.com/20160616KullbackLeibler.pdf …



