一般のランダムウォークに関する逆正弦法則
#数楽 もしかして、ギャンブルに関する逆正弦法則って人気のネタですか?「単純な丁半博打をたくさん繰り返すとき、トータルで浮いている時間の割合の確率密度函数が1/(π√(x(1-x)))dxで近似される」というのが逆正弦法則です。50%が最低で0%と100%の両端で発散している!
#数楽 そういう「遊び」をやっことがある人は「ずっとプラスで浮いている状態を維持できていたり、ずっとマイナスの状態に沈んでいることの方が多くて、トータルで浮いている時間と沈んでいる時間が同じ程度になることは少ない」ということを経験的によく知っているはず。
#数楽 浮いているときには「まだ浮いている」と安心し、沈んでいるときには「ついていない」と嘆きます。安心している時間と嘆いている時間が半々程度になることは稀で、安心している時間の割合の方が高くなったり、嘆いている時間の割合が高くなったりと、偏ることが普通。
#数楽 株式投資や為替投資をやったことのある人はたくさんいると思いますが、幸福な時間の割合が長い人達と嘆いている時間の割合が長い人達の割合が高く、半々程度の人達は少数派のはず。そして、それは実力の問題でもなんでもなくて、単なる確率論的現象だということ。
#数楽 逆正弦分布は円周上の一様分布をx軸上に射影したものです。繰り返しのギャンブル(=ランダムウォークwww)で浮いている時間の割合が円周上の一様分布の射影になっているのは不思議です。何か直観的にわかりやすい説明は有るのでしょうか?
#数楽 ばねで振動している質点の位置をランダムな時間に大量に観測すれば、その位置の分布は逆正弦分布(円周上の一様分布のx軸への射影で得られる分布)になります。ばねが伸び切ったり縮み切ったりしたとき質点の動きは遅くなるので、そういう場所にたくさん分布する。
#数楽 ばね振動での質点の位置の分布が逆正弦分布になるという事実はほとんど逆正弦分布の定義からただちに得られるトートロジーに近い。直観的によくわからないのは、ランダムウォークで原点より右にいる時間の割合も逆正弦分布すること。
#数楽 ギャンブルに関する逆正弦法則は確率論の一般向けの解説では人気のネタのようですが、どうして円周上の一様分布の射影が出て来るかが直観的によくわかる解説をググって見付けることはできませんでした(当然英語でも検索した)。知っている人がいれば教えて下さい。
#数楽 古典ばね振動ではトートロジー的に逆正弦分布が出て来る。量子調和振動子でも、nが大きいとき、n次Hermite多項式の2乗×e^{-x^2/2}が逆正弦分布で近似されるという話は所謂準古典極限に関する物理では定番の話だと思う。

#数楽 ランダムウォークに関する逆正弦法則の解説としてよく引用されているのは Spitzer, Frank. Principles of Random Walk. Springer GTM34 (1964)の§20.pic.twitter.com/jPyQRLM9JG

#数楽 一つ前のツイートの添付画像にはこのツイートの添付画像の問題(6)の解答が書いてあります。添付画像の問題(1),(2),(3)あたりは大学での確率統計の授業の試験問題として採用されている場合が結構ありそう。pic.twitter.com/D1G0yNQAxp
#数楽 一般にレベルXに属する事柄について教えるときには、その一段階上のレベルX+1以上の教養が必要だと思う。たとえば高校レベルの数学を教えるためには本当は大学レベルの数学の知識が必要。高校レベルの数学の話をどこかの輩が勝手に決めた学習指導要領の範囲内の理解で押し通すのは論外。
#数楽 私でもすぐに読めそうな文献で、ランダムウォークの逆正弦法則について調べてみたのですが、「出て来る分布がどうして中心が(x,y)=(1/2,0)で半径が1/2の円周上の一様分布をx軸に射影したものになるか」について直観的な理解は得られませんでした。
#数楽 「原点から出発する左右対称なランダムウォークで時刻nまでに原点より右にいる割合をX_nと書くと、X_nの確率分布はn→∞で中心(1/2,0)半径1/2の円周上の一様分布をx軸に射影したものに収束する」というのが逆正弦法則。計算すると確かにそうなる。
#数楽 単純ランダムウォークの逆正弦法則についてはhttp://c-faculty.chuo-u.ac.jp/~nishioka/2011.html …のランダム・ウォーク-レジメ.pdfにも解説がありますね。
#数楽https://www.google.co.jp/search?q=Spitzer+Principles+of+random+walk …GoogleでSpitzer Principles of random walkを検索。ランダムウォークの逆正弦法則に興味を持った人にとって役に立つ検索。https://twitter.com/genkuroki/status/794153129981800448 …
#数楽 リンクメモhttps://twitter.com/genkuroki/status/795293218569003008 …リンク先の引用中で引用されている一般のランダムウォークに関するE. Sparre Andersenさんの論文→ http://www.mscand.dk/article/view/10385 …
#数楽 fluctuation theoryにおける"Equivalence Principle"の証明http://www.mscand.dk/article/download/11419/9436 …R. Altschul (1972)滅茶苦茶初等的なので「高校レベル」に近いと言えるかも。全単射の概念は使う。
#数楽 リンクメモhttps://www.encyclopediaofmath.org/index.php/Andersen_theorem …Andersen theoremequivalence principlearcsin law
#数楽 リンクメモhttps://en.wikipedia.org/wiki/Arcsine_laws_(Wiener_process) …arcsine law1st. 浮いている時間の割合が逆正弦分布2nd. 最後に打ち沈みが逆転するまでの時間の割合が逆正弦分布3rd. 最も浮いている状態に最初に達するまでの時間の割合が逆正弦分布
#数楽https://www.encyclopediaofmath.org/index.php/Andersen_theorem …http://www.mscand.dk/article/download/11419/9436 …Sparre Andersenの等価原理x_1,…,x_nは実数列とする。n次の置換σ(k)=i_kに対して、s_k(σ)=x_{i_1}+…+x_{i_k}とおく。続く
#数楽 続き。s_k(σ)>0となるk=1,…,nの個数をN_n(σ)と書き、s_1(σ),…,s_n(σ)の最大値にs_k(σ)が等しくなる最初のkをL_n(σ)と書く。N_n(σ)は浮いている時間であり、L_n(σ)は最も浮いている状態に達するまでの時間を意味する。続く
#数楽 続き。等価原理:置換を置換に移す全単射σ→φ(σ)で、N_n(σ)=L_n(φ(σ))を満たすものを具体的に作れる。すなわち、浮いている時間がkの場合と最も浮いている状態に達するまでの時間がkの場合をx_{i_k}の順序を変えることによって一対一に対応させることができる。
#数楽 続き。以上、くそまじめに結果を説明しましたが、以上の「等価原理」には初等的で易しい証明が存在します(高校生でもがんばれば理解できるはず)。対応を直接かつ具体的に作れる。証明の詳細は http://www.mscand.dk/article/download/11419/9436 … にあります。
#数楽 続き。リンク先訂正。一つ前のツイートで紹介した論文には図がないのでhttp://www.mscand.dk/article/download/10668/8689 …にある図も一緒に見た方がわかりやすいと思います。

#数楽 添付画像は一つ前のツイートで紹介した論文より浮いている時間(左図の実線部分)ピークに達するまでの時間(右図の実線部分)が等しいランダムウォークは互いに一対一に対応している。この結果の理解には特別に難しい数学的道具は一切必要ない。完全に初等的。pic.twitter.com/DWGZ9ayGIJ
#数楽 この初等的結果から、浮いている時間の割合が漸近的に逆正弦分布に従うことと、最高に浮いている状態に達するまでの時間の割合が漸近的に逆正弦分布に従うことが同値であることがわかる。浮いている時間の割合も最高に浮いている状態に達するまでの時間の割合も1/2に近いことは稀。

#数楽 pic.twitter.com/DWGZ9ayGIJx→π(x)の逆変換の構成の仕方→π(x)の右端の到達点が正か負(非正)かで、xの方の最後の部分がπ(x)の左端になるか右端になるかが決まることに注意すれば、同じことを繰り返すことによってπ(x)からxを復元できる。

#数楽 pic.twitter.com/DWGZ9ayGIJ添付画像ではこうなる。π(x)の右端が正なので、xの右端も正。ゆえにxの右端はπ(x)の左端に等しい。次π(x)から左端を取り除いたものの出発点を0に移動する。その結果の右端は正なのでxの右端一歩手前も正になる。続く
#数楽 続き。ゆえにxの右端一歩手前はπ(x)の左端になる。その次。π(x)からすでに使った分の2つを取り除いたものの出発点(左端)を0に移動する。すると右端が負になる。ゆえにxの右端から2歩手前はπ(x)の右端に等しい。以下、同様に繰り返せば、π(x)からxを復元できる。

#数楽pic.twitter.com/DWGZ9ayGIJxからのπ(x)の作り方をxの左端から順番に見て行くと、π(x)の方でピークに達する時刻がxの方での浮いている時間に一致することもわかります。
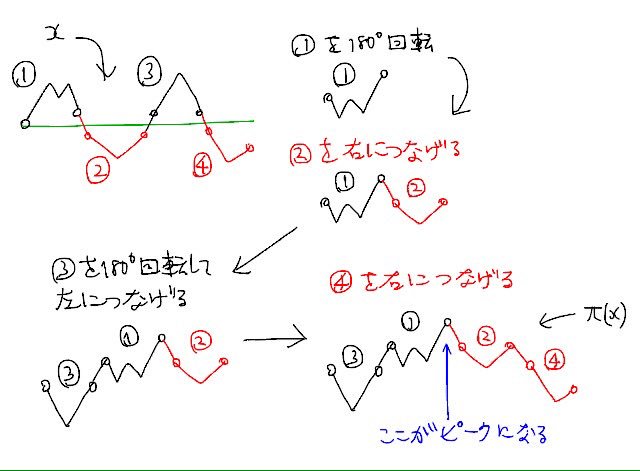
#数楽 xの方で浮いている時間とπ(x)の方でピークに達する最初の時間が一致することは添付画像のように考えればほぼ自明になる。pic.twitter.com/J1L3hK0vGu
#数楽 以上によって、ランダムウォークに関するSparre Andersenの等価原理の証明が完了した!しかも対応の作り方を理解してしまえば初等的かつ直観的に明らかな結果であることもわかった。たぶん、もっと詳しい説明があれば高校生でも理解できる。
#数楽 逆正弦法則に出て来る逆正弦分布はBeta(1/2,1/2)分布に等しい。これは二項分布のベイズ推定のJeffreys事前分布としても有名。円周上の一様分布の射影に等しい分布にもなっています。https://twitter.com/genkuroki/status/795965793762615296 …
#数楽 上の方の説明を読んだ後に原論文 http://www.mscand.dk/article/download/11419/9436 … を見れば、直観的に自明な議論を論文を書くためにどのように正確に言い換えているかがわかると思います。直観的な理解はその逆の作業を行うことに等しい。そういう作業をサボると数学はわからなくなる。
#数楽 乱歩(ランダムウォーク)の話の続き。確率1/2で±1進む単純乱歩だとは限らない一般の1次元乱歩で等価原理を示せたので、逆正弦法則の証明まであと一歩の所まで来ています。そのあと一歩の部分にはちょっとした解析が必要。続く
#数楽 続き。等価原理とは「時刻nまでの間に浮いている時間N_nがkの乱歩」と「時刻nまでの間のピークに達する最初の時刻L_nがkの乱歩」が自然に(特に確率を保ちながら)一対一に対応しているという結果でした。その証明は本質的に確率論とは無関係の完全に初等的なものでした。続く
#数楽 続き。等価原理より、N_n=kとなる確率はL_n=kを満たす乱歩を時刻kの前後に分けてそれぞれの確率の積を取ることによって、P(N_n=k)=P(L_n=k)=P(N_k=k)P(N_{n-k}=0)と書けることがわかります。この公式は任意の乱歩で成立。続く
#数楽 続き。残りの問題はP(N_k=k)とP(N_{n-k}=0)の漸近挙動を調べること。N_k=kは「時刻kまでに浮いている時間がkとなること」すなわち時刻kまでずっと浮きっぱなしを意味し、同様にしてN_k=0は時刻kまで全く浮かないことを意味しています。続く
#数楽 続き。それらの確率を乱歩S_n=X_1+…+X_nに関する確率で表す公式がある!Σq^k P(N_k=k)=exp(Σ(q^n/n)P(S_n>0)),Σq^k P(N_k=0)=exp(Σ(q^n/n)P(S_n≦0)).ここでk≧0,n>0.続く
#数楽 続きexp(Σ(q^n/n)(1/2))=1/√(1-q)であり、そのqに関する展開のk次の係数はbinom(2k,k)/4^kになり、Wallisの公式よりそれは~1/√(πk)を満たします。もしもS_k>0(≧0)となる確率が1/2なら実際にそうなり、続く
#数楽 続き、それに近い状況でも、展開の係数の漸近挙動は同じになります。(Tauber型定理を使う。) こんな感じで単純乱歩とは限らない乱歩の場合にも逆正弦法則が拡張されます。続く
#数楽 続き。等価原理は初等的に証明できるので、逆正弦法則の証明はΣq^k P(N_k=k)=exp(Σ(q^n/n)P(S_n>0))などの公式の証明に帰着します。この公式も初等的な証明があると思うのですが、現時点の私はわからない。初等的証明にこだわらなければ、~続く
#数楽 続き~、パラメーターをもう1つ増やした公式Σq^k E[e^{itS_k}1_{N_k=k}]=exp(Σ(q^n/n)E[e^{itS_n}1_{S_n>0}])の証明に帰着するという方法で示せます(t=0の場合が示したい公式)。証明は簡単ですが、理解はしていない。
#数楽 続き。公式Σq^k P(N_k=k)=exp(Σ(q^n/n)P(S_n>0))の右辺はq=uのように変数名を変えれば合同ゼータ函数の定義に似ています(確率P(S_n>0)が有理点の個数に対応) 。関係があるかどうかについて、現時点での私は知らない。
#数楽 すでに誰かが通った道であれば、証明や計算ができるようになることは勉強に費やす時間の問題に過ぎない。しかし、証明や計算はできる。だが、理解はしていない!となることが実に多いと思う。


#数楽 公式Σv^k P(N_k=k)=exp(Σ(v^n/n)P(S_n>0))(一つ前のツイートの公式は誤植を含む)の証明、その2/2pic.twitter.com/VsnrmnJYT6
#数楽 続き。証明のポイントは2つ。和S_kの特性函数の母函数をS_kが初めて0以下になる時刻Tの前後に分割すること。0より大きな実数全体に台が含まれる分布と0以下の実数全体に台が含まれる分布の共通部分が0だけであることとフーリエ変換変換が単射であることを使うこと。
#数楽 続き。P(S_n>0)=1/2+ε_n、Σε_n=log aと仮定する。このときv↑1でΣv^k P(N_k=k)=exp(Σ(q^v/n)P(S_n>0))〜a/√(1-v).Tauber 型定理より、k→∞でP(N_k=k)〜a/√(πk).
#数楽 続き。同様にしてΣv^k P(N_k=0)=exp(Σ(q^v/n)P(S_n≦0))〜a^{-1}/√(1-v).Tauber 型定理より、k→∞でP(N_k=0)〜a^{-1}/√(πk).
#数楽 続き。ゆえに等価原理より、P(N_n=k)=P(N_k=k)P(N_{n-k}=0)〜1/(π√(k(n-k)))=(1/π) dx/√(x(1-x)).ここでx=k/n、dx=1/nとおいた。これは逆正弦分布の確率密度函数。これが逆正弦法則。
#数楽 ここで使ったTauber型定理についてはhttp://www.math.tohoku.ac.jp/~kuroki/LaTeX/20160501StirlingFormula.pdf …の第10節を見て下さい。
#数楽 http://www.math.tohoku.ac.jp/~kuroki/LaTeX/20160501StirlingFormula.pdf …使用したTauber型定理は系10.6です。
#数楽 https://mobile.twitter.com/genkuroki/status/798217401020006401 …リンク先の議論を自明な方法で一般化すると、逆正弦分布より少し一般的な、確率密度函数がx^{p-1}(1-x)^{-p}/B(p,1-p)の形の分布も得られます。続く
#数楽 P(S_n>0)=1/p+ε_n、Σε_n=log aと仮定する。このときv↑1でΣv^k P(N_k=k)=exp(Σ(q^v/n)P(S_n>0))〜a/(1-v)^p.Tauber型定理より、k→∞でP(N_k=k)〜ak^{p-1}/Γ(p).
#数楽 続き。同様にしてΣv^k P(N_k=0)=exp(Σ(q^v/n)P(S_n≦0))〜a^{-1}/(1-v)^{1-p}Tauber 型定理より、k→∞でP(N_k=0)〜a^{-1}k^{-p}/Γ(1-p).
#数楽 続き。ゆえに等価原理より、P(N_n=k)=P(N_k=k)P(N_{n-k}=0)〜k^{p-1}(n-k)^{-p}/Γ(p)Γ(1-p)=x^{p-1}(1-x)^{-p}dx/B(p,1-p)ここでx=k/n、dx=1/nとおいた。
#数楽 大雑把に言えば、要するに、n→∞で勝っている確率がpならば、浮いている時間の割合の確率分布は近似的にBeta(p,1-p)分布になるということです。問題:iidの和について可能なpの値は?
#数楽 次のノートを追加した。http://www.math.tohoku.ac.jp/~kuroki/LaTeX/#2016-11-02 …→ http://www.math.tohoku.ac.jp/~kuroki/LaTeX/20161102ArcSineLawForSimpleRandomWalks.pdf …単純ランダムウォークの逆正弦法則 (手書きのノート)次のまとめの添付画像をPDFにまとめたものhttps://twitter.com/genkuroki/status/795079149882732544 …
#数楽 現在 http://math.tohoku.ac.jp/~kuroki/LaTeX/ にアクセスできなくなっています。最近ずっと使いまわしている解説のコピーを以下の場所に置いておきました。http://genkuroki.web.fc2.com/20160501StirlingFormula.pdf …http://genkuroki.web.fc2.com/20160616KullbackLeibler.pdf …



