「高校数学における三角函数の微積分は循環論法になっている」というデマについて
#数楽 ちょっと高校数学での三角函数の定義について疑問を持っている人を見つけたので、以前した話を繰り返します。問題の中心はラジアンによる角度の定義です。しかし、高校数学IIIまでやれば曲線の長さを積分で表わす公式を習うので、それを使えばすべてがうまく行きます。続く
#数楽 高校数学IIIで習う公式(曲線の長さ)=∫_a^b √(x'(t)^2+y'(t)^2)dtを使えば単位円周上の弧の長さを積分で書くことができます。だから単位円周上の弧の長さで定義されるラジアンの意味での角度が明瞭に定義されます。続く
#数楽 単位円周をx=√(1-t^2)、y=tとパラメトライズするとき、θ(s)=∫0^s√(x'(t)^2+y'(t)^2)dt=∫_0^s dt/√(1-t^2)は単位円周上の(1,0)から(√(1-s^2),s)までの角度。続く
#数楽 続き。だから、θ=θ(s)の逆函数は高1で習うs=sin θの定義に一致しています。逆函数の微分の計算の仕方もわかっているので、sin θも簡単に微分できます。sinを微分するためにlim_{θ→0}(sin θ)/θ=1はいらない。続く
#数楽 続き。以上の話は真に高校数学の範囲内の話です。lim_{θ→0}(sin θ)/θ=1を使わずにsinを微分し放題なことが高校数学の範囲内でわかるので、lim_{θ→0}(sin θ)/θの計算でもロピタルの定理を使っても循環論法になりません。続く
#数楽 続き。高校生は以上の事柄について高校の数学の先生に聞いた方がよいかもしれません。当たり前のことだという反応が返って来ない場合にはその先生は三角函数論を理解していないとみなされます。大学の数学の先生の中にも循環論法になると誤解している人達がいるかも。
#数楽 私の経験では三角函数について「循環論法になる」というようなことを言う人は自分できちんと三角函数論を展開したことがなくて、自信がない人達なのではないかと思われます。自信があればデマに騙されたり、影響されずに済んでいるはず。
#数楽 単位円周のシンプルなパラメトライズの方法は他にもあります。x^2+x^2=1とy=sxの交点をsでパラメトライズすると、x=1√/(1+s^2)、y=s/√(1+s^2)なので、円弧の長さをsによる積分であらわすと、〜続く
#数楽 続き〜、θ(t)=∫_0^t ds/(1+s^2) となり、これは傾き0からsまでの角度になります。θ=θ(t)の逆函数は高1で習うt=tan θの定義に一致します。これを使うとtan θの導函数が1+tan^2θになることも直ちにわかる。
#数楽 積分で角度を表わしておいてその逆函数で三角函数を定義することは、ラジアンの意味での角度で三角函数を定義する高校数学のやり方をきちんと説明しているとみなせます。この考え方が普及していないので「循環論法」とか言う困った人達が出て来るのだと思う。
#数楽 第1種楕円積分は∫0^z dt/√((1-t^2)(1-k^2t^2))という形なので、k^2=0,1の特別な場合として、arc sin と arc tanh を含んでいます。
#数楽 そうそう、ロピタルの定理を使うと減点されるとかなんとかは全てくだらない話。以上で説明したような事柄を理解していることが大事。そして大学入試なんかでは自分がきちんと理解していることがわかるように書くことが大事。理解していてかつ説明できることが大事。
#数楽 個人的な希望としては、高校生くらいになったら「問題の解答を書く」というスタイルはきちんとゴミ箱に捨てて、自分の考え方をきちんとわかりやすく説明しようと努力する姿勢を身に付けて欲しい。数学を使うときには「問題の解答を書く」というスタイルにならないです。
#数楽 数学の筆記試験が必要な大学を受験するということは、数学の試験を通過できるだけではなく、道具として数学をある程度使いこなせないと困る場所に行くということです。最初からそこを目標にして勉強した方が本物の知識が身につくので効率が良いと思います。
#数楽 単に試験を通過するためだけに数学の勉強をしようとしても「これ、自分の人生に何の役に立つの?」となってモチベーションは下がりがちだと思います。そして、文系学部に進んで、統計学が必要になったり、経済学を理解する必要が出て来たときに後悔することになる。
#数楽 あとググると、三角函数の「循環論法に陥らない導入法」の説明が、cosとsinを天下り的にべき級数で定義する流儀が非常に目立つような気がする。高校数学っぽく、円弧の長さで角度を定義して三角函数を定義しても全然困らないことも知っておかないとまずいです。
#数楽 高校数学っぽく、円弧の長さ(積分で定義できる)で角度を定義して三角函数を導入するスタイルでは、逆函数の微分法によって三角函数の導函数は定義から簡単に計算できる。少なくとも、教える側にとっては当然の常識でなければ困ると思う。
#数楽 この件に定期的に触れているのは、大学の数学の先生達の中には無用に「循環論法」という説を拡散して誤解を広めている人達がいるから。今回は具体的な名前は出さないですが、ツイッターの過去ログを見れば名前を出してそれはまずいんじゃないかと言っています。
#数楽 リンク先の公式はすべて幾何学的な意味をわかっていれば「明らか」な公式です。暗記は無用。各種教科書(大学新入生向けのものを含む)を見た感じでは、そういうことをきちんと解説してある教科書はまれなのではないかと思う。解説に続くhttps://twitter.com/EOzv5/status/825681447675523072 …
#数楽 続き。まず、三角函数系の積分公式は円周上の弧の長さや扇型の面積を積分で表わす公式に過ぎません。何の長さや面積を表わしているかと三角函数の定義を知っていればそこから公式が当たり前の公式として出て来る。ただし、必要な被積分函数の形の決定には若干の計算が必要。続く
#数楽 続き。次に、双曲線函数系の積分公式では、面積の方で考えれば新しいアイデアは必要ないのですが( https://ja.wikipedia.org/wiki/双曲線関数 … )、三角函数での「弧の長さ」の類似を考えるためには曲線の「長さ」をローレンツ計量で測るというアイデアが必要になります。続く
#数楽 例:直線y=txとx^2+y^2=1の交点(1/√(1+t^2),t/√(1+t^2))を考え、そのt=0からt=aまでの軌跡(円弧)の長さ(傾きaの角度)はθ=⌠_0^a dt/(1+t^2)となる(計算せよ)。tanの定義よりa=tan θ、θ=arc tan θ.
#数楽 例:x^2+y^2=1上の点(√(1-t^2),t)のt=0からt=yまでの軌跡(円弧)の長さ(角度)はθ=∫_0^y dy/√(1-y^2)となることが計算で確認できる(高校数学IIIレベルの話)。sinの定義よりy=sin θ、θ=arc sin y.
#数楽 これで⌠dt/(1+t^2)と⌠dy/√(1-y^2)の公式は、それらが単位円弧の長さを表わす積分なのでtanやsinの定義から「明らか」であり、暗記の必要はないことがわかった。円弧の長さがそのように書けること自体数学的に結構重要。楕円積分の話に自然に繋がる。続く
#数楽 例:適切に図を描けば、0<y=sin θ<1、θ=arc sin yのとき⌠_0^y √(1-t^2)dt=(三角形の面積)+(扇型の面積)=y√(1-y^2)/2+θ/2=(1/2)(y√(1-y^2)+arc sin y)となることは明らかである。
#数楽 以上に三角函数(すなわち円)が関係する3つの積分公式は「円弧の長さ」や「三角形と扇型を合わせたものの面積」を表わす「明らかな公式」に過ぎないことがわかった。ちょっとした計算は必要だが、本質的に三角函数の定義から直接的に(置換積分抜きに)出て来る公式に過ぎない。
#数楽 「数学では基本が大事。定義まで戻ってよく考えてみよう」というようなことがよく言われるのは、以上のようなことが少なくないからです。ある人は「面倒な置換積分が必要だ」と思っているのに、別の人は「三角函数の定義より明らか」と思っている。その二人の理解度には大差がついている。
#数楽 本当はクリスタル・クリアーな理解が可能なのに、ややこしい考え方をしてしまう。これはよくあることです。私もよくある。仕方がないと思います。しかし、クリスタル・クリアーな理解がどういうことなのかを何度も経験しておくことはとても大事なことだと思う。
#数楽 双曲線x^2-y^2=1に関係する双曲線函数について理解するためには、双曲線からどのように「ローレンツ計量」が自然に出て来るかを理解する必要があります。どうするのが「普通」なのか私は知らないのですが(何が「普通」なのかを知らずに全部自分で考えることが基本)、~続く
#数楽 続き。双曲線上x^2-y^2=1上の微小に離れた点(x,y)、(x+dx,y+dy)と原点(0,0)で囲まれる三角形の面積dSを計算すると、x dx-y dy=0 より(2dS)^2=dy^2-dx^2になること分かります。右辺に「ローレンツ計量」が出て来ている。続く
#数楽 続き。dθ=2dSとおいて、dθ^2=dy^2-dx^2と式を整理しておきます(微小円弧の長さdθに関するdθ^2=dx^2+dy^2の類似公式)。x=cosh t=(e^t+1/e^t)/2、y=sinh t=(e^t-1/e^t)/2とおくとdθ^2=dt^2。続く
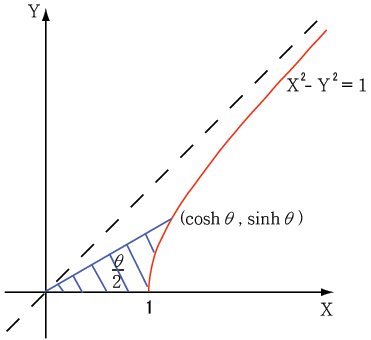
#数楽 続き。すなわち、(x,y)=(cosh t, sinh t)という双曲線x^2-y^2=1のパラメーター表示のパラメーターtは添付画像のθに一致していることが確認できました。添付画像は https://ja.wikipedia.org/wiki/双曲線関数 … より。pic.twitter.com/C7jnYZR3n3
#数楽 例:適切に図を描けば、0<y=sinh θ、θ=arc sinh yのとき⌠_0^y √(1+t^2)dt=(三角形の面積)+(斜線部分の面積)=y√(1+y^2)/2+θ/2=(1/2)(y√(1+y^2)+arc sinh y)となることは明らかである。
#数楽 注意:一つ前のツイートの積分変数tは(x,y)=(cosh t,sinh t)と置いたときのtではなく、(x,y)=(√(1+t^2),t)と置いたときのtであることに注意せよ。これで⌠√(1+t^2)dtの公式の2つの項の幾何的な意味が「明らか」になったわけです。
#数楽 例:(x,y)=(√(1+t^2),t)とおいて、dθ=√(dy^2-dx^2)をt=0からt=y=sinh θまで積分した結果はθになるので、少し計算すると∫_0^y dt/√(1+t^2)=θ=arc sinh yとなることがわかります。
#数楽 例:y=tx (0≦t<1)とx^2-y^2=1の交点(x,y)=(1/√(1-t^2),t/√(1-t^2))を考えることによって、一つ前の例と同様にして⌠_0^a dt/(1-t^2) = θ = arc tanh aとなることもわかります。
#数楽 ⌠dt/√(1+t^2)、⌠dt/(1-t^2)は双曲線上の弧の「ローレンツ計量」に関する「長さ」(固有時間)を表し、⌠√(1+t^2)dtは三角形と斜線部分を合わせた部分の面積を表わすことがわかりました。(紹介した計算は「ローレンツ計量」を知らなくても全部理解可能)
#数楽 以上で紹介した計算は「ローレンツ計量」について何も知らなくてもすべて高校数学IIIの範囲内までですべて理解可能なはずです。しかし、双曲線函数と「ローレンツ計量」が関係あるということを知っていると特殊相対性理論を勉強するときに役に立ちます。特殊相対性理論も理系の教養の一つ。
#数楽 以上のような話を全部書いてある高校生向け参考書または大学新入生向けの教科書ってありますか?私は見たことがない。「基本に忠実で定義まで戻ってクリスタルクリアな理解を目指すことは当然だ」とされているので、わざわざ教科書に書くまでないということになっているのでしょうかね。

#数楽 あと、何度も言って来たことですが、高校数学IIIの教科書には昔から曲線の長さを積分で表せることが載っています。しかし、その取り扱いはとても小さくて、ラジアンの意味での角度がどのようにそれによって正当化されるかさえ何も書かれていない。pic.twitter.com/cQd0TuYD5r
#数楽 ググると「高校数学における三角関数の取り扱いは循環論法になっている」という有害な都市伝説の存在に気付きます。大学の数学の先生の一部がその都市伝説の源泉になっている疑いもあり、非常に嘆かわしいことだと思っています。続く
#数楽 続き。「曲線の長さは折れ線近似で定義しなければいけない」と誤解していたり、「三角関数を厳密に定義するためにはべき級数で定義するのがよい」という発想にとらわれている人が検索すると結構容易に見つかる。どうしてこんなことになっているのか。とても残念なことです。
#数楽 続き。y=sin θをθ=∫_0^y dt/√(1-t^2)の逆函数として定義する、θが単位円の弧の長さであることから、θがラジアンの意味での角度を意味することがわかり、その方針でのsin θの定義は高校数学でのsin θの定義に一致していることがわかります。続く
#数楽 続き。θ(y)=∫_0^y dt/√(1-t^2)が単位円の弧の長さであることは、x(t)=√(1-t^2)、y(t)=tに曲線の長さの積分表示を適用すればすぐにわかります。θ'(y)=1/√(1-y^2)から逆函数の導関数として(sin θ)'=cos θがすぐに出る。
#数楽 続き。要するに、lim_{θ→0}((sin x)/x)=1を示すことに三角関数の導関数の計算を帰着する方針はものすごく遠回りしているわけです。「単位円上の点のy座標を弧長の長さの函数とみなしたもの」というsin θの定義から直接出る計算を小難しくやっているだけ。続く
#数楽 続き。応用と無関係に「どのような定式化にすれば理論全体がすっきりきれいにまとまるか」という視点も数学ではとても重要です。思考の節約をするために定式化を工夫するという発想の気持ち良さを納得できる例として、単位円の弧長の積分表示から出発する三角関数論の展開は重要だと思う。
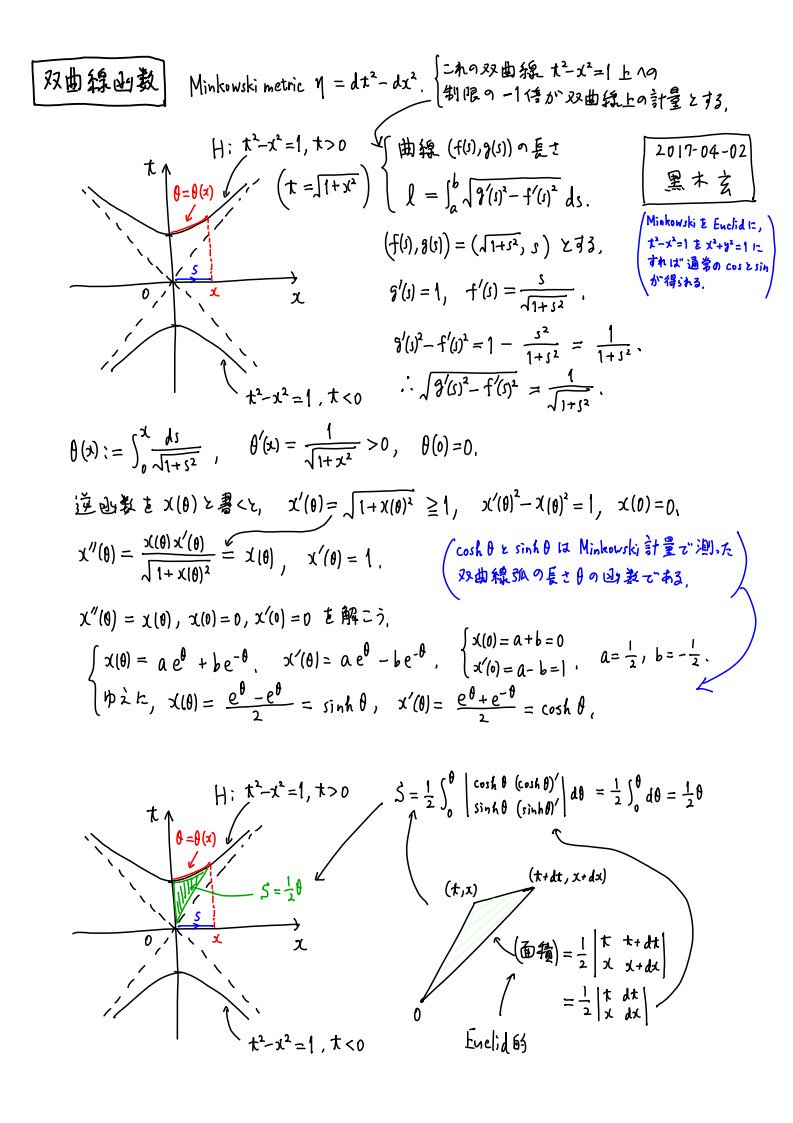
#数楽 sinh θのような双曲線函数は、三角函数論において長さをユークリッド的に測っていた部分をミンコフスキー計量に置き換えるだけで、得られます。双曲線函数におけるθはミンコフスキー計量で測った双曲線上の弧長の長さになっています。ユークリッドとミンコフスキーの違い。pic.twitter.com/g4fVDWh3my
#数楽 三角函数論も双曲線函数論も「不定積分で定義された函数の逆函数で函数を定義すると有用な函数が得られる」という普遍的なパターンの特別な場合。楕円函数論は被積分函数を1/√(3次または4次函数)とすれば同じ方針で得られます。ただし本質を理解するためには複素函数論が必須になる。
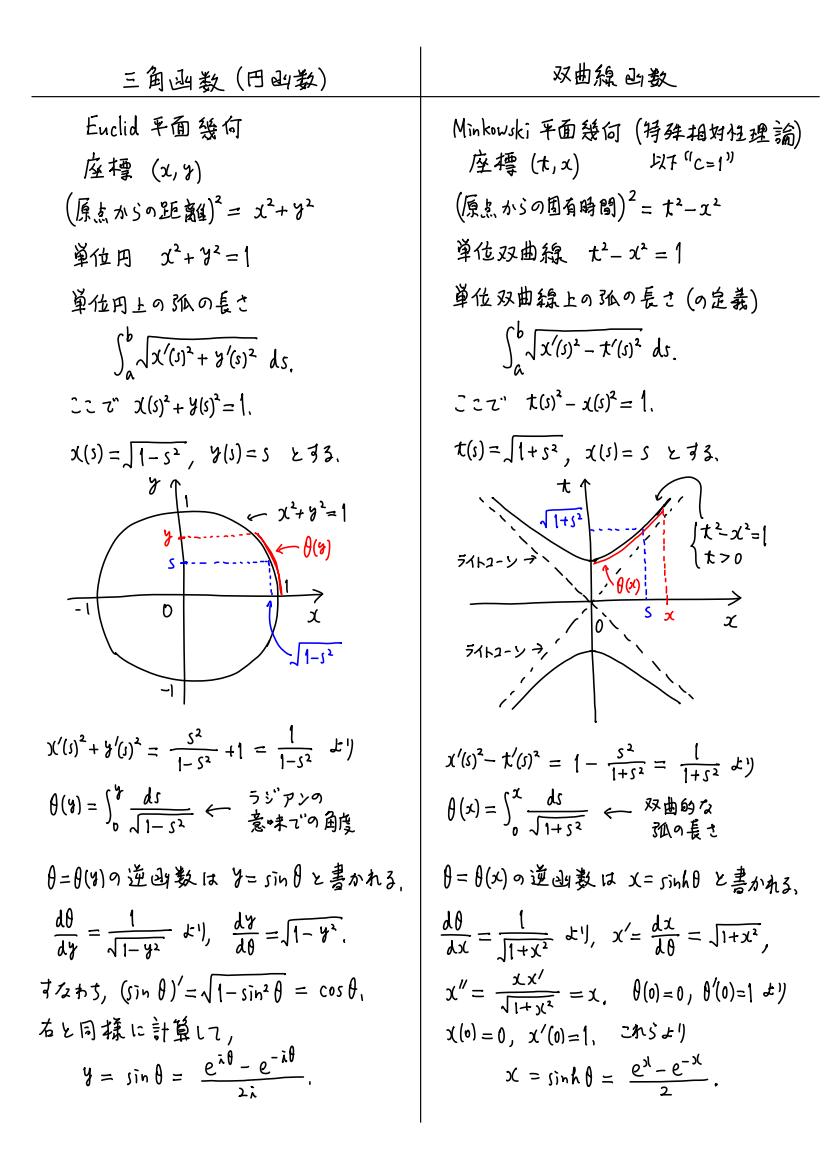
#数楽 https://twitter.com/genkuroki/status/848444518030430209 … に情報追加。三角函数(円函数)と双曲線函数の比較。この手のノートを自分で作りまくるのが数学の勉強の一つのスタイル。計算用紙を大量に消費することになる。pic.twitter.com/bZzE8jE9Ku

#数楽 微分dy/dxを何の誤差も無くdy÷dxだとみなす方法の話について補足。高木貞治『解析概論』p.36より【dy=f'(x)dx (1)そのようにdy,dxを単独に定義すれば,(1)の意味は明確である.】pic.twitter.com/U0SGPEBQx7

#数楽 続き。高木貞治『解析概論』p.37より【記号dy/dxにおいてdxおよびdyが各々独立の意味を有するから,dy/dxは商として意味を有する.】『解析概論』では微分の導入段階で最初から「dy/dxは商として意味を有する」となっています。pic.twitter.com/syPf8qvzR4
#数楽 高木貞治『解析概論』のような本には微分の導入段階で「dy/dxは商として意味を有する」と書いてあります。「dy/dxは分数(商)ではない」と言う数学の先生はきっと『解析概論』レベルの数学の本で勉強したことがないのでしょう。生徒の側は先生に厳しく突っ込みを入れるべきです。
三角函数と双曲線函数の微積分の基礎付けについては次のリンク先を見て下さい。「径路の長さが速さの積分で書けること」と「逆函数の導函数」からsinの微分がcosになることがすぐに出ます。面積経由は無用なステップを増やしているだけ。https://twitter.com/genkuroki/status/848918996275548160 …
角度は単位円弧の長さ∫_0^y ds/√(1-s^2)で定義され、扇型の面積は∫_0^y √(1-s^2) ds-y√(1-y^2)/2になるのですが、扇型の面積を角度で表すためには前者で後者を表すことになります。単に余計な手間が増えるだけです。
リンク先は双曲線函数に関する解説ですが、三角函数も同様であり、返答連鎖の前後に色々書いてあります。https://mobile.twitter.com/genkuroki/status/848444518030430209 …
#数楽 高校レベルの積分の計算問題関係の話がリンク先のモーメントにまとまっています。最近の高校の数学の教科書の様子も少し紹介してあります。https://twitter.com/i/moments/848450692645662720 …
「三角函数の微積分は高校数学の範囲内では循環論法になっている」という話は多分大学の数学の先生が流したデマです。曲線の長さを折れ線近似で考えるのは面倒だと言う理由で、リンク先のように積分一発で定義してしまって全然問題ありません。https://twitter.com/genkuroki/status/848918996275548160 …
高1で習う三角関数の定義では円弧の長さがきちんと定義されていないのですが、高校数学IIIで曲線の長さが積分で書けることをやるので、高1での三角関数の定義がそのまま正当化され、そこから直接sinの導函数がcosになることが直接出ます。sin x/xの極限の話をするのはひどい遠回り。
「曲線の長さを積分一発で書かずに折れ線近似にこだわる」とか「三角関数をべき級数で定義することにこだわる」というようなタイプの解説が結構多くてよくない感じ。実際には、高1で習う三角関数の定義が積分論によって直接正当化され、sinの導函数は逆函数の導函数の特別な場合に過ぎません。
あと「dy/dxは分数(商)ではない」というデマも大流行中なんですが、大昔からみんな参照しているはずの高木貞治『解析概論』には【dy/dxは商として意味を有する】としっかり書いてあったりする。何がどうなっているんだか。https://twitter.com/genkuroki/status/851671745178124288 …
#数楽 "「高校数学における三角函数の微積分は循環論法になっている」というデマについて"https://twitter.com/i/moments/857377316032307200 …



