#数楽 問題:実数yと正の整数nに対してf_n(y)=(y>-√nのとき e^{-√n y}(1+√n y/n)^n、y≦-√nのとき0)と定める。lim_{n→∞}f_n(y)を求めよ。これはよい試験問題だったようだ。http://www.wolframalpha.com/input/?i=\lim_{n\to\infty}+e**{-\sqrt{n}y}(1+\sqrt{n}y/n)**n …
#数楽 任意の実数yに対して十分nを大きくすればy>-√nとなるので、y>-√nと仮定してよいということを見抜かないといけない。あとはlog f_n(y)=-√n y+n log(1+y/√n)のn→∞での極限を求めるだけ。Taylorの定理(もしくは展開)を使えば簡単。
#数楽 log(1+x)=x-x^2/(2(1+θ(x)x)^2) (0<θ(x)<1) を使うと、log f_n(y)=-√n y+n log(1+y/√n)=-y^2/(2(1+θ(y/√n)y/√n)^2)→-y^2/2なのでf_n(y)→e^{-y^2/2}.
#数楽 もしくは、n→∞のとき、log f_n(y)=-√n y+n log(1+y/√n)=-√n y+n(y/√n-y^2/(2n)+y^3/(3n√n)-y^4/(4n^2)+…)=-y^2/2+y^3/(3√n)-y^4/(4n)+…→-y^2/2.
#数楽 問題:√2 sin(π/4+0.1)を小数点以下第5桁目まで求めよ。第6桁目以降は四捨五入せずに切り捨てよ。これは易しい問題。0.1についてTaylor展開すれば易しい算数レベルの計算になる。http://www.wolframalpha.com/input/?i=�%88�2+\sin(\pi/4+0.1 …)
#数楽 「10の[イ]乗分の1未満」の[イ]を埋めさせる問題を出したら、正解は6なのに-6と書いている人がいた場合には、「問題の読み間違いに過ぎない。実質的に理解しているとみなせる」と好意的に解釈して正解とすることにするかな。
#数楽 問題:p_i, q_i は正の実数であり、Σ_{i=1}^r p_i=Σ_{i=1}^r q_i=1であるとする。このときΣ_{i=1}^r p_i log(p_i/q_i)≧0であることを証明せよ。Jensenの不等式を覚えている人は認めて使ってよい。J不等式一発。
#数楽 「f(x)=x log x、x>0とおくと、f''(x)=1/x>0なのでf(x)は下に凸である。ゆえにJensenの不等式より、Σp_i log(p_i/q_i)=Σq_i f(p_i/q_i)≧f(Σq_i(p_i/q_i))=f(1)=0」で満点。
#数楽 Jensenの不等式を知らなくても、「x log x が下に凸なことより、x log x≧x-1 (x>0)なので、Σp_i log(p_i/q_i)=Σq_i(p_i/q_i)log(p_i/q_i)≧Σq_i(p_i/q_i-1)=0」で満点。高校レベルの問題。
#数楽 Σ p_i log(p_i/q_i) はKullback-Leibler情報量と呼ばれており、それが0以上になることはGIbbsの不等式と呼ばれているらしい。どういう名前が付いているかはどうでもよいことだが、自然に出て来る大事な量であることを知っておくのはとてもよいこと。
#数楽 問題:α>0とする。f_α(p)=∫_{-∞}^∞ e^{-x^2/α} cos(px) dx を計算せよ。ガウス積分∫_{-∞}^∞ e^{-x^2/α} dx=√(απ)などは既知としてよい。これはガウス分布のフーリエ変換。知らないと困る人が多いはず。
#数楽 e^{-x^2/α}のフーリエ変換は√(απ)e^{-αp^2/4}.1つ目の方法:cos(px)をべき級数展開して無限和と積分を交換して、∫_{-∞}^∞ e^{-x^2/α} x^{2k} dx=√(πα)(2k)!α^k/(4^k k!)を使う。
#数楽 ∫_{-∞}^∞ e^{-x^2/α} x^{2k} dx=√(πα)(2k)!α^k/(4^k k!) は0~∞の積分の2倍に等しく、 x=√(αt)とおくと、正の半整数でのガンマ函数に帰着できる。ガンマ函数を知らなくても様々な方法で計算できる。
#数楽 WolframAlphaで exp(-x^2/a) のフーリエ変換を計算するにはこうすればよい→ http://www.wolframalpha.com/input/?i=�%88�_{-∞}**∞+exp(-x^2/a)+cos(px)+dx+where+a>0 … (where a>0 と書いておくことがポイント。しっかり√(aπ) e^{-ap^2/4} と計算してくれている。)
#数楽 2つ目の計算法:f_α(p)をpで微分。微分と積分を交換して、部分積分すると、f_α'(p)=(-p/2)f_α(p)となることがわかる。ガウス積分の公式よりf_α(0)=√(απ)なので、微分方程式を解いて、f_α(p)=√(απ) e^{-p^2/4}.
#数楽 問題:a,bは正の実数であるとする。積分 2∫_0^{π/2}(sin θ)^{a-1}(cos θ)^{b-1}dθ をベータ函数 B(p,q)=∫_0^1 x^{p-1}(1-x)^{q-1} dx (p,q>0)を用いて表わせ。これはサービス問題のつもり。
#数楽 ベータ函数の定義式の方で試しに x=(sin θ)^2 と置けば答えがわかる。一つ前の問題の答えは B(a/2,b/2) です。(sin θ)^2=x に気付くかどうかだけの簡単な問題。
#数楽 問題:2∫_0^{π/2} (sin θ)^6 (cos θ)^4 dθ を求めよ。これもサービス問題。6と4をもっと巨大な数にしようと思ったが、サービス問題にするために止めた。ベータ函数の知識がなくても高校レベルの直接的な計算でも求まる。
#数楽 一つ前のツイートの2つ目のリンクの仕方がおかしくなってしまった。括弧閉じるが抜けた。しかし、WolframAlphaさんは賢いので勝手に括弧閉じるをおぎなって正解してくれている。答えは B(7/2,5/2)=3π/256.
#数楽 問題:nは正の整数であるとする。実数xの実数値函数f(x)はn回微分可能であるとし、x,hは実数であるとする。Mは正の実数であるとし、xとx+hのあいだの任意の次数ξについて|f^{(n)}(ξ)|≦Mが成立していると仮定する。このとき~続く
#数楽 続き~Taylorの定理より、|f(x+h)-Σ_{k=0}^{n-1} f^{(k)}(x)h^k/k!|≦[ア]が成立する。[ア]に書くべきMを含む式を答えよ。答えは Mh^n/n!.Taylorの定理は誤差評価のためにこの形で使われること多い。
#数楽 問題続き:この不等式をf(x)=e^x、x=0、h=1、M=e、n=10の場合に適用すると、1/0!+1/1!+1/2!+…+1/9!とe=2.718281828…の差の絶対値は10の[イ]乗分の1未満になることがわかる。[イ]に書き込める最大の整数を答えよ。
#数楽 問題続き:9!=362880を用いてよい。e/10!<1/10^6なので6が答え。厳密にはTaylorの定理から得られる誤差の上からの評価で最大の整数が得られているかどうかは確認が必要なのだが、答えがあっていれば全部マルにする。
#数楽 ε-δで講義をしていなくても、誤差の大きさを評価できないようでは理系の人間として困るはずなので、こういう問題を出している。Taylorの定理、部分積分、フーリエ解析、凸解析などは様々な評価(不等式)を出すための基本だと思う。
#数楽 ε-δを教えるときに単に数学的に厳密になるだけだと教わる側にとってありがたみが少ないし、講義をする側もやっていてつまらないのではないかと思う。様々な量の評価(上からおよび下からの評価)ができて、漸近挙動を分析できるところまで連れて行きたい。しかし、現実には夢のような話。
#数楽 数学の授業は教える側が本気を出して自分が面白いと感じるような話をやりたいようにやってしまうと、教わる側にとって難解すぎて悲惨なことになるのが常だと思う。しかし教える側がつまらない話をルーチンで説明するだけの授業も悲惨。私ならそういう講義には出ない(実際に出なかった)。
#数楽 http://www.wolframalpha.com/input/?i=\lim_{n\to\infty}+e**{-\sqrt{n}y}(1+\sqrt{n}y/n)**n …リンク先の極限を求める問題は微妙にひっかけ問題になっている。(1+√n y/N)^NでN→∞とするとe^{√n y}になり、e^{-√n y}と掛け合わせると1になる。そういう計算は間違った答えを出す。続く
#数楽 その間違った答えを出す計算はlogを取った後のTaylor展開の1次の項までしか見ていない計算と同値になる。2次まで見ないと正しい答えが出ない。この極限の問題の出処はStirlingの公式の証明。n!=∫_0^∞ e^{-x} x^n dx で~続く
続き~x=n+√n y=n(1+y/√n)で置換積分すると、n!=n^n e^{-n}√n ∫_{-√n}^∞ e^{-√n y}(1+y/√n)^n dyとなり、積分部分はn→∞で∫_R e^{-y^2/2} dy=√(2π)に収束する。Stirlingの公式が証明された。
#数楽 問題を出す側は感覚が麻痺していて、どれがどのように難しい問題なのかわからないまま問題を出している。多くの数学教師が試験後に「しまった」「やってしまった」と後悔している。
#数楽 以上で色々紹介したWolframAlphaでの計算例を見れば、大学1年レベルの微積分の計算問題の多くがWolframAlphaで簡単に解けることがわかると思う。線形代数の方も同様である。WolframAlphaは非常に便利。
#数楽 f(x)=x log xのときのΣq_i f(p_i/q_i)=Σp_i log(p_i/q_i)はKullback-Leibler divergenceと、一般のfに対するΣq_i f(p_i/q_i)はCsiszar f-divergenceと呼ばれているらしい。
#数楽 WolframAlphaは数式のTeX記法を理解してくれるのでTeXは知っておいて損がないです。しかし、twitterでURLを引用したければ上付きを^ではなく**と表記した方がよいです。例→ http://www.wolframalpha.com/input/?i=\lim_{n\to\infty}+e**{-\sqrt{n}y}(1+\sqrt{n}y/n)**n …
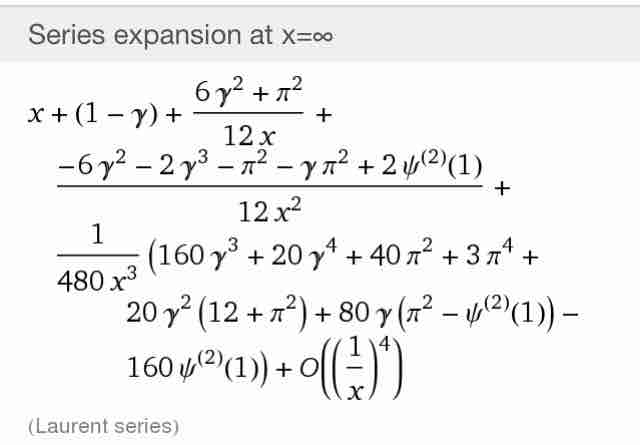
Re:RThttps://twitter.com/iwaokimura/status/761484925858045952 …WolframAlphaさんにΓ(1/(x+1))について質問してみた。ほんとだ!http://www.wolframalpha.com/input/?i=series of Γ(1/(x+1))? …pic.twitter.com/dC8cI7X0sk
あれ?リンク先がおかしい?+が欠けた。これならどうかな?http://www.wolframalpha.com/input/?i=series+of+Γ(1/(x+1))? …#数楽
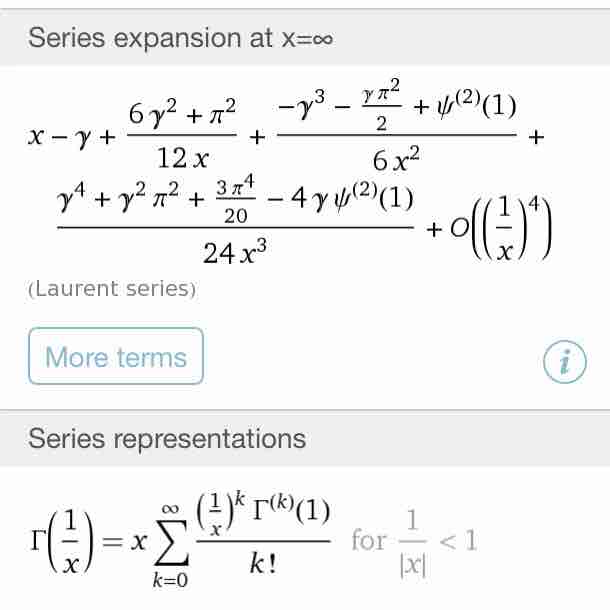
#数楽 ううむ。+が欠けるので、Γ(1/x)について聞いてみることにする。 http://www.wolframalpha.com/input/?i=series+of+Γ(1/x)? …pic.twitter.com/IL9TXvXC1u
#数楽 実数xが大きなとき、Γ(1/x)はx-γでよく近似されるんですね。知らなかった。ここでγはオイラー定数。π=3.141592653…e=2.718281828…γ=0.5772156649…くらいは暗記してもバチが当たらない。
#数楽 私はWolframAlphaをiPhoneでの有料アプリ経由で使うことが大部分。web経由で無料で利用する場合よりもCPUを余計に使ってたくさんの情報を返してくれます。これにはお金を出す価値があると思う。
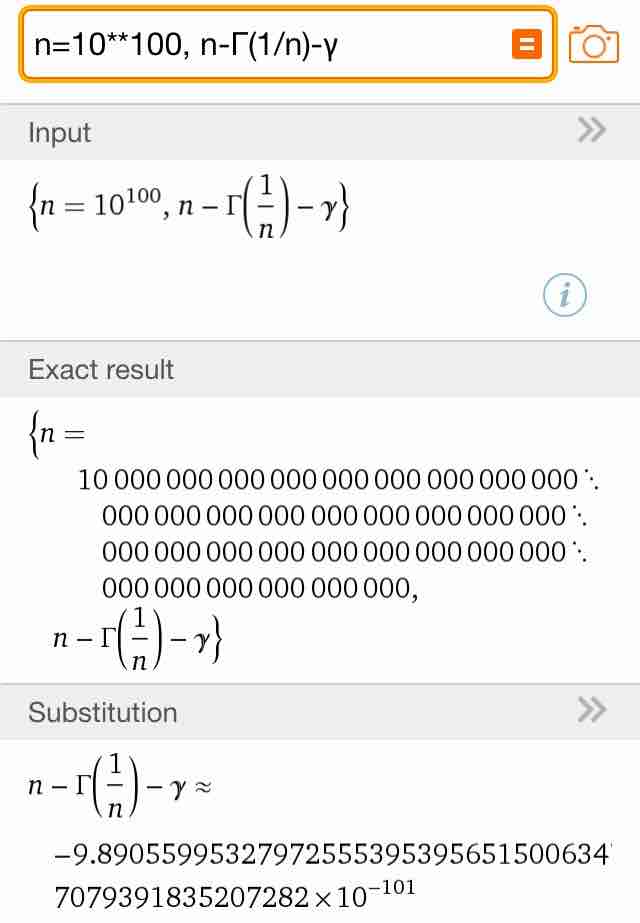
#数楽http://www.wolframalpha.com/input/?i=n=10**100, n-Γ(1/n)-γ …n=10^100 のときにΓ(1/n)とn−γの差を計算。WolframAlphaさんによれば差の絶対値は10^100分の1未満になるみたい。pic.twitter.com/g2iF3wYouf
Γ'(1)= -γを覚えておれば x Γ(x)= Γ(1+x) ≒1-γ x よりΓ(1/n)≒n-γ まではすぐにわかりますが剰余項の評価を真面目にやるのが面倒かも、nが十分大きい時、ならよいのですが。
#数楽Γ(1/x)=x-γ+O(1/x) as x→∞についてhttps://twitter.com/Paul_Painleve/status/761684290740498433 …Γ(x)のx→0での様子を見るという話は、Γ(x)=Γ(1+x)/xより、Γ(1+x)のx→0での様子を見るという話と同じ。
黒木さんのガンマ函数の展開が気になった。Γ(1+x)のマクローリン展開は直接計算すると複雑だが、Γ函数の対数微分であるディガンマ函数ψ(x)ならΓ函数の積展開から容易にψ(x+1)のマクローリン係数がζ函数になることが示される https://ja.wikipedia.org/wiki/ディガンマ関数 … (続
たとえば、ψ'(1)=ζ(2)=π^2/6である。ψ'(x)=d^2[log[Γ(x)]]/dx^2 =Γ''(x)/Γ(x)-Γ'(x)^2/Γ(x)^2 なのでΓ(1)=1.Γ'(1)=-γを使ってΓ''(1)=Γ'(x)^2+ψ'(1)=γ^2+π^2/6 となる (続
2次以下の展開もζ(n)で書けてるがMathematicaはζの奇数での特殊値を避けているので表示がわかりにくい https://twitter.com/genkuroki/status/761556989642104832 … (終
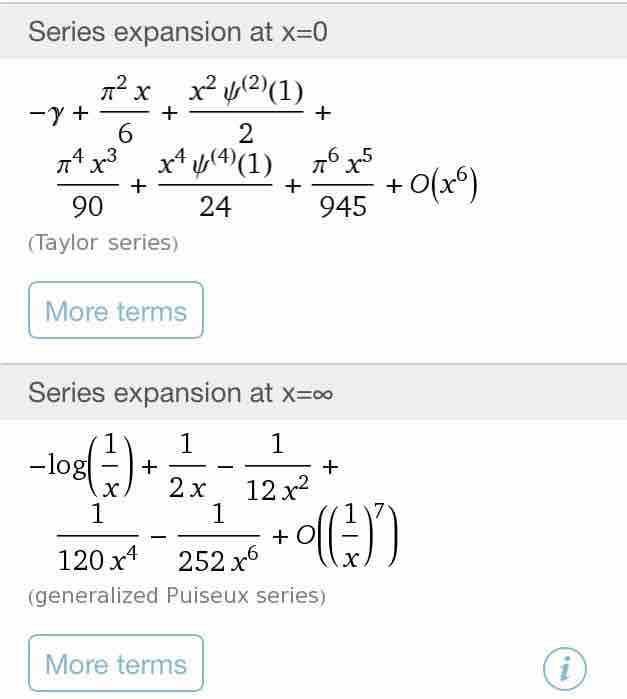
Re:RTs WolframAlphaさんがディガンマ函数を知っているようなので、こう聞いてみた→ series of ψ(1+x)? http://www.wolframalpha.com/input/?i=series of ψ(1+x)? …やはりゼータで書いてはくれない。pic.twitter.com/6dESBp4qUI

#数楽 「きりのよい積分」で表示できる数は特別な重要性を持っていると思われています。たとえば2∫_{-1}^1 √(1-t^2) dt=πや∫_0^1(∫_0^x 1/(x(1-y)) dy)dx=ζ(2) http://www.wolframalpha.com/input/?i= %E2��_0**1(∫_0**x 1/(x(1-y)) dy)dx …
Re:RT 俺の新入生向け微積授業では必ずやる話。例として√10=3.162…の計算なんかはよくやる。|x|<1ならば(1+x)^a=1+ax+a(a-1)x^2/2+a(a-1)(a-2)x^3/3!+…と√9=3を使う。 #数楽
#数楽 二項展開を使うより、ニュートン法を使った方が圧倒的に収束が速いのですが、精密な値ではなく2〜3桁程度を求めればよいならば、二項展開を暗算で使った方が楽。一次近似や二次近似を「現場でさらりとできる」とちょっとかっこいいと思う。
#数楽 工学部の規模は大きいので新入生向けの授業は工学部向けを担当せよと言われることが多いのですが、工学部生の*くせ*に一次近似、二次近似という言葉の意味を理解してなかったり、実際に使えなかったりするのはとてもまずいと思う。
#数楽 「工学部生の*くせ*に」とあおってみましたが、新入生の段階では焦る必要は全然なくて、経験値を高める機会を増やす努力をしながら数年待てば、自分には不可能だと思っていたことが自然にできるようになっているはず。
#数楽WolframAlphaで√10の近似計算3(1+ax+a(a-1)x**2/2+a(a-1)(a-2)x^3/3!) where a=1/2 and x=1/9http://www.wolframalpha.com/input/?i=3(1%2bax+a(a-1)x**2/2+a(a-1)(a-2)x^3/3!) where a=1/2 and x=1/9 …
#数楽√10 = √(9+1)=3√(1+1/9)=3(1+(1/2)(1/9)+(1/2)(1/2-1)(1/9)^2/2+…)1/9≒0.1とみなして一次近似で切ると√10≒3(1+0.1/2)=3.15となります(暗算容易!)。結構いい近似。
#数楽 実用的には一次近似で足りることが多いよね。日常生活内で平方根を計算したくなるケースについては→ http://togetter.com/li/823134 大阪都構想の出口調査の結果を見て平方根を計算する人



