三角函数の加法公式

#数楽 高校生および大学新入生向け
「三角函数の加法公式について説明して!」と頼まれたら添付画像程度の図は描けて欲しい。pic.twitter.com/UzQveMZ7zy
#数楽 誤解しているかもしれませんが、高校の数学の教科書で三角函数の加法公式は余弦定理を使って証明していたと思います( https://www.google.co.jp/search?q=%E4%BD%99%E5%BC%A6%E5%AE%9A%E7%90%86+%E4%B8%89%E8%A7%92%E9%96%A2%E6%95%B0%E3%81%AE%E5%8A%A0%E6%B3%95%E5%AE%9A%E7%90%86&tbm=isch … )。私はあの証明が嫌い。三角函数の定義だけに基いて公式を出せるのに遠回りをしているように感じられます。
#数楽 もしかしたら、角度に制限を付けて場合分けをしたりする必要がないというような理由で余弦定理を使って「両辺を比較する」タイプの証明を載せているのかもしれませんが、そのレベルでの厳密性へのこだわりは正直言ってあんまり意味がないと思う。
#数楽 三角函数の加法公式は「図を描いて角度や長さが分かる部分について順番に式を書き込んで行く」という基本中の基本で何のアイデアもいらない話のはずなのに、「余弦定理を使って証明する」というように「誤解」したままの高校生や大学新入生は多いのではないだろうか?
#数楽 2×2の回転行列Qに対するA=(E-Q)/(E+Q)の計算は複素数でやった方が楽な人が多いと思う。q=e^{it}のとき分子分母をe^{it/2}で割って整理すると、a=(1-q)/(1+q)=-i tan(t/2). 続くhttps://twitter.com/genkuroki/status/842900777978929152 …
#数楽 続き。Aは-i tan(t/2)に対応する2×2行列で、
A=(E-Q)(E+Q)^{-1}=
[ 0 tan(θ/2)]
[-tan(θ/2) 0 ].
1は2×2の単位行列に対応し、虚数単位iは
[ 0 1]
[-1 0]
に対応。
#数楽 Cayley変換の応用:q=e^{iθ}のときa=(1-q)/(1+q)=-i tan(θ/2)、q=(1-a)/(1+a)から、よく使われる有理化の公式「t=tan(θ/2)とおくとcos θ=(1-t^2)/(1+t^2)、sin θ=2t/(1+t^2)」が出ます。

#数楽 ちなみにtan(θ/2)の正体は「xy平面上の原点を中心とする単位円周の点(cos θ, sin θ)における接線と直線x=1の交点のy座標」です。図を描くと合同な直角三角形が見えるのでθ/2が出て来る理由がわかる。pic.twitter.com/ZlUXKm7SCj
#数楽 訂正:以上の話の流儀では、虚数単位iに対応しているのは、
[ 0 1]
[-1 0]
ではなく、
I=
[0 -1]
[1 0]
の方。このIについて
exp(θI)=(cos θ)E+(sin θ)Ihttps://twitter.com/genkuroki/status/843073702946197505 …
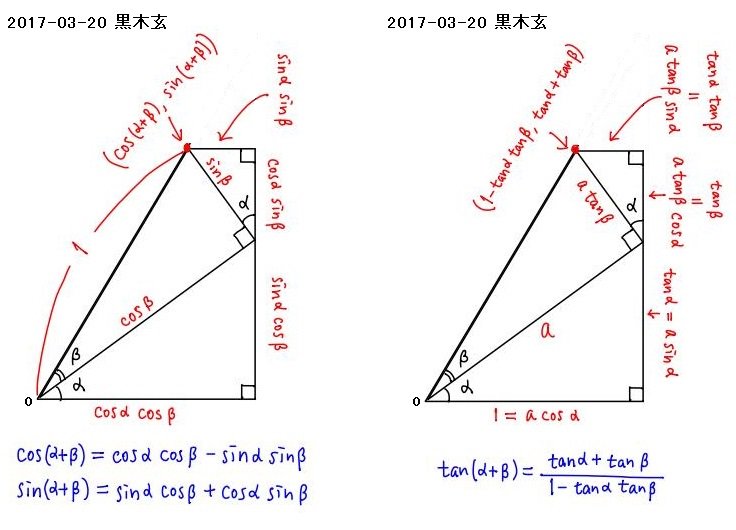

#数楽 tan(α+β)の分母1-tan α tan βと分子tan α+tan βを座標に持つ点がどこにあるかを示す図もあんまり見ることがないよね。pic.twitter.com/8jlZXR27HV
#数楽 ibisPaintX (iPad)というアプリで作成した三角函数の加法公式の図を描く様子の動画。pic.twitter.com/pi7h2xhnGR
#数楽 三角函数の加法公式の導出は三角比の定義を習った直後にやる適切な練習問題だと思う。角度をどのように測るかとは無関係に図を描くだけで三角比のあいだの関係式として導出可能。試行錯誤を一週間程度続ければ(そういうことを真剣にすることは難しい)、自力で発見できる人は結構いると思う。
#数楽 何をやったら良いのかさえわからない状態から、延々と試行錯誤を積み重ねる思考法を小学生の段階で徹底的に教えて欲しいのだが、現実はそういうのとは逆方向の算数教育になってしまっている。何をやって良いかさえわからない状況が怖くないという事実は経験しないと一生わからないと思う。
#数楽 三角函数の加法公式などなどについて大量の知識を教えてもらった後であっても、試行錯誤のネタは常に大量に残っている。だから、自力で導出することが困難な話をさらりと教えてしまうこと自体には問題がない。面白い試行錯誤のネタは尽きることがないという事実の認識が重要。
#数楽 @sekibunnteisuu 三角函数は解析函数なので、一致の定理より、角度α,βがα≧0,β≧0,α+β≦0の特殊な場合だけ証明しておけば、一般の場合の証明にもなっています。
#数楽 子供のときからずっとボールを投げて遊んだことがない人がボールの投げ方の解説を見ただかでボールをうまく投げられるようになることはありえない。自分で実際にボールを投げることを繰り返す練習が必須。数学も全く同じだし、図を描いて考えることも同じ。実際には何でもそうだと思う。
#数楽 ボールをうまく投げることはかなり複雑で精妙な動きを体に覚えさせる必要が有るのですが、紙とペンを使った数学的試行錯誤もまた相当に複雑で精妙な頭の使い方が必要になります。子供のときから何度も実際にやった経験を積み重ねないとおそらく一生の間身につかない。
#数楽 高校生のあいだもしくは大学に入学するまでの三角関数の加法定理は「証明は定義に基いて瞬殺」となっていて欲しいので、証明の図を一つ紹介しました。そして試行錯誤の重要性を強調した。その二つの話には当然繋がりがあります。続く
#数楽 三角函数の定義しか知らない人が自力で三角函数の加法公式を試行錯誤で発見しようとしたら、様々な図が描かれることになるでしょう。実は、この場合には、どれか一つの図が「正解」と言うことにはならず、「どれでも実りある結果が得られる」という仕組みになっています。続く

#数楽 続き。三角比の定義しか知らない人が角度αと角度βに関する三角函数の加法公式について調べようとすると、2つの直角三角形を角度α+βが様々な形で連結した図を描くことになるでしょう。実はそのどれであっても三角函数の加法公式を示せます。pic.twitter.com/slmXWMeNJK



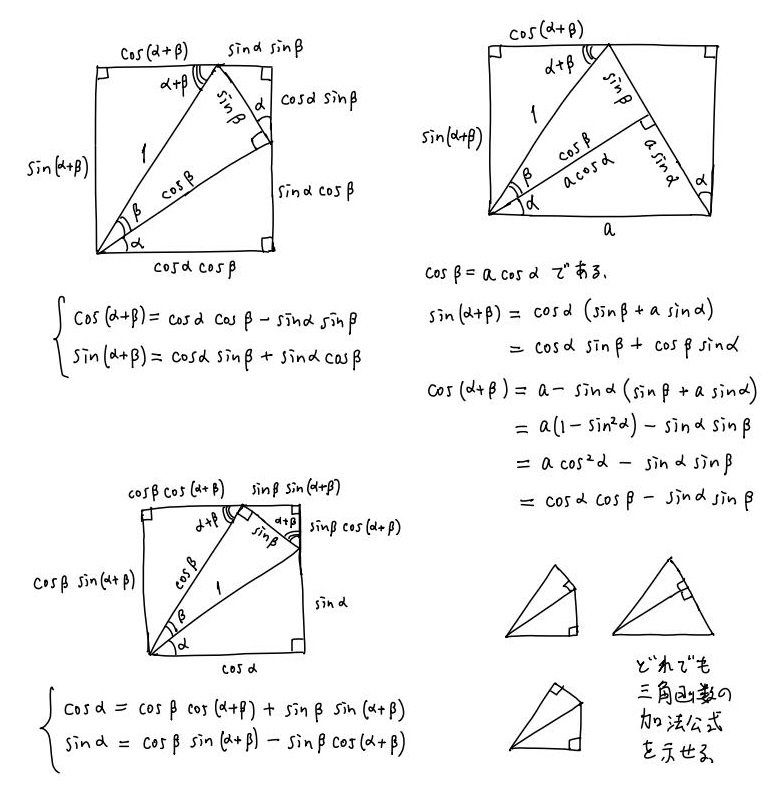
#数楽 以上の内容を一枚の画像で
三角函数の加法定理の三角函数の定義しか使わない証明は様々な図で可能である!pic.twitter.com/tKAHVESBBM
#数楽 余弦定理も正弦定理もトレミーの定理も何も使わずに、複数の作図で三角函数の加法定理は証明可能です。だから、「自力で三角函数の加法定理を発見すること」は試行錯誤のとてもよい題材なのです。あれでも、これでも、それでもよい。しかも飛び道具は一切いらない。
#数楽 補足:cosとsinは解析函数なので、一致の定理より、角度αとβがどちらも正で和が90°より小さい場合に加法公式を証明しておけば、それだけで一般の場合の証明が完了したことになる。こういう事情があるので、そういう場合に制限しても失われるものは実質的にない。
#数楽
トレミーの定理:円に内接する四角形の2本の対角線の長さの積は対辺の積の和に等しい。
これは実は次のように書き直せます。
公式:sin(α+β)sin(β+γ)=sin(α+β+γ)sin β+sin α sin γ
β+γ=90°の場合がsinの加法公式です。
#数楽 一つ前のツイートの三つの角度に関するsinの加法公式(トレミーの定理を書き直したもの)はsinの通常の加法公式を特別な場合に含み、逆にsinの通常の加法公式から一つ前のツイートの三つの角度に関するsinの加法公式(本質的にトレミーの定理)を簡単に示せます。

#数楽 だから、トレミー(Ptolemy)の定理は実質的にsinの通常の加法公式と本質的に同等のことを言っているということになります。pic.twitter.com/q73s9xaMi4
#数楽 トレミーの定理は円に内接する四角形や三角形を扱っているので、トレミーの定理と三角函数の関係について語る場合には、正弦定理を前もって証明しておいて(易しい)、空気のごとく使うことにしないと苦しいです。
#数楽 トレミーの定理は21世紀になってからクラスター代数関係の数学に登場して結構活躍したので、21世紀になってからトレミーの定理の重要性を再認識した数学者は結構多いと思います。https://www.google.co.jp/search?num=100&q=(%22%E3%83%88%E3%83%AC%E3%83%9F%E3%83%BC%E3%81%AE%E5%AE%9A%E7%90%86%22++OR+Ptolemy)+(%22%E3%82%AF%E3%83%A9%E3%82%B9%E3%82%BF%E3%83%BC%E4%BB%A3%E6%95%B0%22+OR+%22cluster+algebras%22)&oq=(%22%E3%83%88%E3%83%AC%E3%83%9F%E3%83%BC%E3%81%AE%E5%AE%9A%E7%90%86%22++OR+Ptolemy)+(%22%E3%82%AF%E3%83%A9%E3%82%B9%E3%82%BF%E3%83%BC%E4%BB%A3%E6%95%B0%22+OR+%22cluster+algebras%22)%20 …
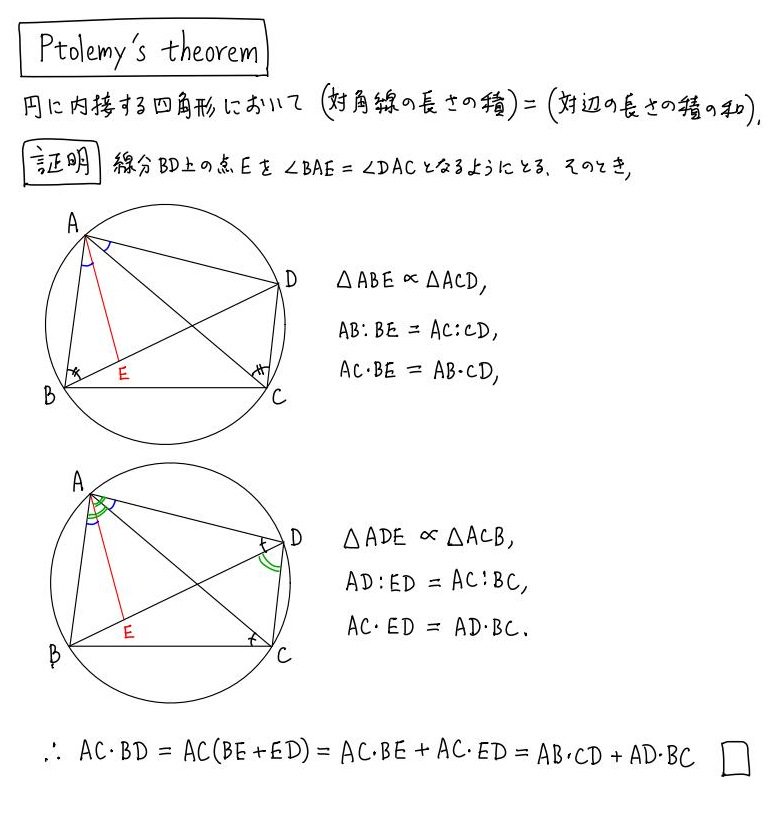
#数楽 私も21世紀になってからトレミーの定理の証明を勉強し直しました。添付画像をトレミーの定理のよく見る証明。すでに紹介したようにトレミーの定理からsinの加法公式が出ることは自明。トレミーの定理は実質的にsinの加法公式そのもの。pic.twitter.com/G23iGV0mr2
#数楽 トレミーの定理は xx'=yy'+zz'の形をしています。その形の公式で有名なものにはグラスマン多様体に関するプリュッカー関係式があります。だから行列式が関係して来る。様々な数学がそこに関係して来て、クラスター代数という21世紀初頭を代表する数学の一つになりました。
#数楽 以上のような21世紀の数学事情があるので、トレミーの定理は単にsinの加法公式と同等な定理とみなして終わりにするのではなく、それ自体が様々な数学を接合する特別な価値を持っていたと考えるべきだと思われます。トレミーさん=プトレマイオスさんもびっくりしていることでしょう。

#数楽 プトレマイオスさんは、三角函数表(現代的には実質的にsin(θ/2)の数表)を作るときに、sinの加法公式に当たるものをトレミー(Ptolemy)の定理から出して使ったようです。sinの加法公式をトレミーの定理から出す証明は「数学史的な証明法」と言えるかもしれません。
#数楽 プトレマイオス(Ptolemy)さんによるトレミー(Ptolemy)の定理の使い方の解説のリンク(三角函数表を作るときに使った)
https://en.wikipedia.org/wiki/Ptolemy%27s_table_of_chords …http://hypertextbook.com/eworld/chords/
#数楽 プトレマイオスさんによるトレミーの定理の使い方の解説
https://books.google.co.jp/books?id=8eaHxE9jUrwC&pg=PA56&lpg=PA56&dq=Ptolemy+%22table+of+chords%22f#v=onepage&q=Ptolemy%20%22table%20of%20chords%22f&f=false …
リンク先のp.58のFig.3.4がトレミーの定理の図。トレミーの定理は実質的に三角函数の加法定理として使用されている。
#数楽 プトレマイオスさんは自身の定理(トレミーの定理)を実質的に三角函数の加法定理として利用しましたが、トレミーの定理の「広い範囲の数学と関係している」(クラスター代数)という意味での重要性は三角函数の加法定理との関係にこだわると見えて来ないので要注意かも。
うげげげげ。「トレミーの定理」についてググると「トレミーの定理を大学入試で使ってよいのですか?」のようないつものくだらない質問が目立つな。日本の数学教育の闇だな、そういう傾向は。こっちは「プトレマイオスの三角函数表」や「クラスター代数」の純粋に面白い話だと思っているんだが。
#数楽 個人的には、プトレマイオスの定理(トレミーの定理)は三角函数の加法定理よりもずっと広い数学と関係する話だと宣伝した方がよいと思う。プトレマイオスの定理経由の加法定理の証明は回転との関係も見難い。三角函数の加法定理は三角比の定義から直接かつ容易に示せ、回転との関係も見易い。
#数楽 大事なポイントは「三角函数の加法定理は難しい話だ」という感覚自体がひどい誤解だということ。プトレマイオスの定理(トレミーの定理)を使った巧妙な方法に目を奪われるとその辺を誤解する可能性がある。まあ、トレミーの定理も三角函数の加法定理も中学生レベルの超易しい話なのですが。
#数楽 三角函数の加法定理も中学生レベルの易しい話だと書いたのは書き間違えではない。三角函数の厳密な定義と無関係に、ある種の長さ達の関係式としての三角函数の加法定理は完全に中学校レベルの数学。cosとかsinのような記号法を使っていることに騙されてはいけない。ものすごく易しい話。
同意します。リア厨2のとき(クラスメートの兄から借りた)高校の数学2Bの参考書に同様の図があって(α、β、α+βがともに0からπ/2のときは)加法定理が成り立つことが納得できますた。 #数楽https://twitter.com/genkuroki/status/844354134773923840 …

#数楽 訂正版。添付画像の「C'」を「E'」に訂正。
三角函数の加法定理はcosやsinという書き方をしなければ中学生レベルの話。そういう易しい話が数学的に重要な役目を果たすことはよくある。pic.twitter.com/ZXauIWu2ih












 バットマン演じた米俳優のA・ウェスト氏が死去 など朝のエンタメニュース10
バットマン演じた米俳優のA・ウェスト氏が死去 など朝のエンタメニュース10


