『わくわく算数2下指導書. 第2部(詳説)』。新興出版社啓林館。2011年。

指導書朱註17頁、教科書17頁。

つまずきと対策 正しく立式するために

 ここでは、「いくつ分」の量が先に、基準量が後に示された適用題を扱い、「基準量のいくつ分」というかけ算の意味についての理解を深めさせる。

 [1]*のような問題では、児童は数値の与えられた順に立式してしまう（4×5とする）ことが多い。題意をしっかりとらえ、基準量が何なのかを判断し、正しく立式できるようにするためには、数図ブロックによる操作や図をうまく活用させるとよい。また、これまでに取り組んだ適用題と比較させ、示された数値の順序の違いを見つけさせることも、基準量を意識させるためには有効である。

 ここでは、かけられる数とかける数の意味がしっかりとらえられているかを評価したい。

*（「基準量」が後に示された問題と朱書きあり）おかしの はこが 4つ あります。 1つの はこには、 おかしが ５こずつ はいって います。 みんなで 何こに なりますか。

何この いくつ分かを考えましょう。（図：●が縦5×横4に並ぶ。5つずつの列が間隔をあけて、4列並んでいるように見える） （挿絵の女の子：しきは、5×4かな4×5かな・・・・・・）（解説文：1つ分の 数は 5で、その 4つ分だから、 しきは 5×4に なります。）

つまずきと対策の文言をそっくりそのまま朱註2005:17に見出す。文章題も同じ。イラストに僅少な異同。

ここでいう数図ブロックの操作とは、このようにタイルの行や列を間を空けて配置することであり、アレイ図と区別されるらしい。

数図ブロックとは：http://www.shinko-keirin.co.jp/keirinkan/sansu/WebHelp/01/page1_03.html

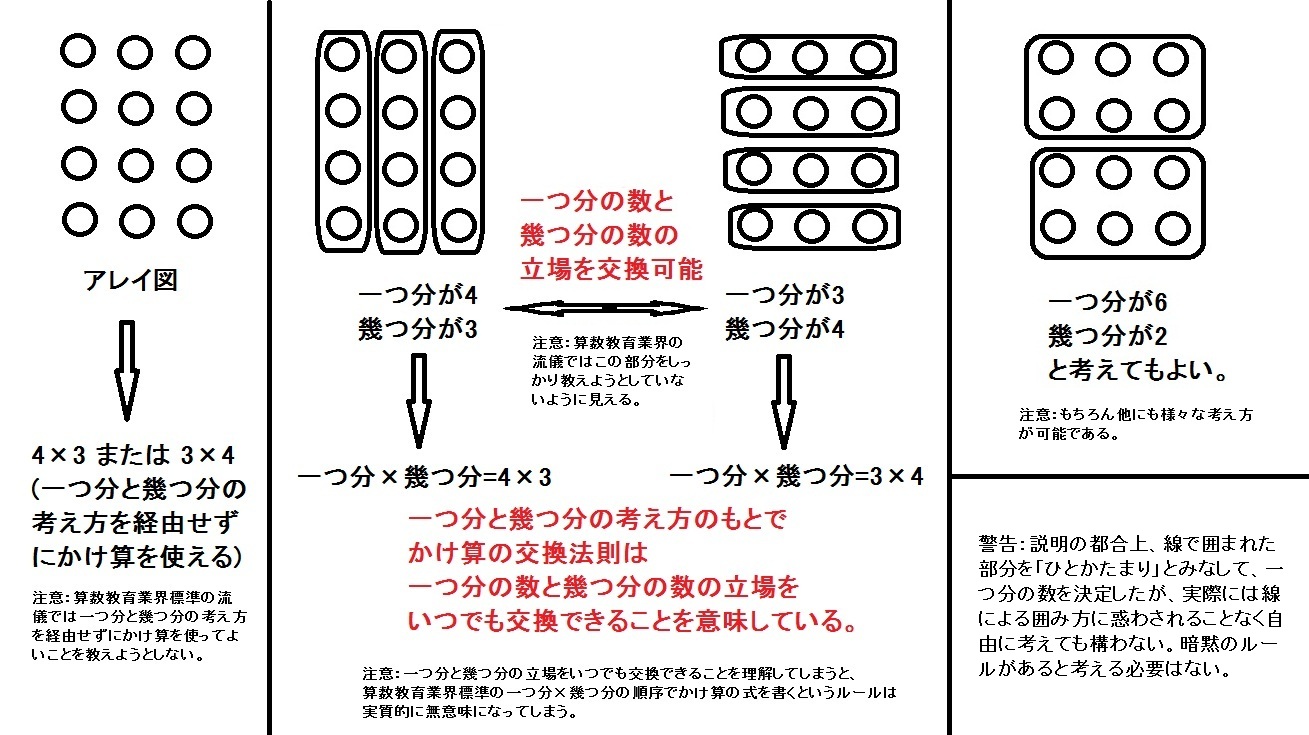
出典：http://genkuroki.web.fc2.com/sansu/#kokanhosoku

半具体物を方形に並べてできる形が同じでも、縦の列と列の間に間隔をあける数図と、横の行と行の間に間隔をあける数図の違いを強調する。挿絵の女の子の発問（「しきは、5×4かな4×5かな」）を考慮に入れれば、黒木玄氏の図にいう「一つ分の数と幾つ分の数の立場を交換可能」であることを教えることは、予定されていないと考えることができる。

第14時のねらい

（略）

場面を数図ブロックで表し、「何個のいくつ分」かを明らかにし、式と答えをかき込む。 15分

手立て

・数図ブロックで問題場面を表させることによって「何個のいくつ分（何倍）」かをわかりやすくさせる。

・数図ブロックの操作から、式が5×4になることをしっかりとらえさせる。

・ノートに5×4になるわけを記述させる。

適用題では、基準量が後に示される場合があることを知る。 5分

・問題文から「何個のいくつ分（何倍）」かをしっかりとらえさせることが大切であることをおさえる。

[考] [技]基準量が後に示された適用題を解くことができる。 《発言・ノート》

(2) (3) （テープを4本、あめを３こ） 基準量が後に示された適用題を解く。 5分

・図や数図ブロックなどを使って(2)では「3cmの4倍」の長さを、(3)では「5円の3倍」の代金を求めることをしっかりとらえさせる。

別冊 1 指導資料集39頁。

単元の指導の要点 > 9 かけ算 (1) > 単元の解説 (p.2～p.21) > I. かけ算の しき > かけ算の意味と式、かけ算と累加・・・・・・p.5

 小単元1(白抜き数字)では、かけ算の意味理解について、「具体的な場面」「半具体物（数図ブロックによる操作）」「ことばでの表現(4の3つ分)」「式での表現(4×3)」「累加で答えを求めること(4+4+4)」の5つの段階を追って進めていくようにしている。この5つについて十分理解できるように、ていねいに指導を進めたい。

p.5

 注意しておきたいことは、「累加=かけ算」と考えてしまわないようにすることである。整数のかけ算と累加の関係については、抽象的にいえば、自然数倍は累加にほかならないが、実際的な意味からいうと、まったく同一のものではない。例えば、「兄は50円の鉛筆を、弟は50円のノートを、妹は50円の消しゴムを買った」というとき、買い物全体の値段は、50+50+50(円)である。これは50×3として計算することができるが、このことがら自体は、たし算であってかけ算ではない。教科書では、かけ算の意味を1つ分の大きさが同じでそれがいくつ分かあるとき、全体の大きさを求めることとしている。したがって、「同じ大きさのもの」が「いくつ分」とおさえ、その結果の求め方として同数累加を用いるよう、かけ算と累加を区別して取り扱っている。同数累加の簡便算としてかけ算を意味づけているのではないのである。

「兄は50円の鉛筆を、弟は50円のノートを、妹は50円の消しゴムを買った」場合の買い物全体の値段が、「50×3として計算することができる」にもかかわらず、「たし算であってかけ算ではない」ことの意味は、この段落にある説述を全て考慮してもなお不明である。可能性としては兄、弟、妹の三人が登場するからなのか、買ったものの種類が違うからなのか、その両方なのかであろう。しかし、登場人物や買った品物についての描写は、合計支払い金額を求めるという見地に立てば、捨象して問題ないから、これらの瑣末な区別によってかけ算で考えることを禁止するのは専断に過ぎる。また、「このことがら自体」が指示する対象が50+50+50(円)であって、この買い物を文章題として解くとき、かけ算を使うことを禁止するものではない可能性もある。しかし、ひとつ分といくつ分の数を認識して、その結果を同数累加で計算するというとき、50+50+50が同数累加を行う式なのか、ひとつ分といくつ分の数をとらえた式なのかは、限定することはできず、「かけ算と累加を区別」することに意義があるという主張は、十分に論証されたとはいえない。

別冊 1 指導資料集44頁。

「基準量」が後に示された問題の立式・・・・・・p.17

 かけ算の適用題は、多くの場合、その文章のなかで「基準量」が先に示されている。しかし、乗数にあたる「いくつ分」が先に示され、被乗数にあたる「基準量」が後に示されることもある。このような場合、問題文を十分に読まずに、示されている数値の順に立式してしまいがちである。[1]では、「はこが 4つ」という表現が、基準量の「5こ」よりも先に示されているので、4×5と立式してしまうのである。

（図：教科書17頁より。既述）

 このような誤りをなくすためには、問題文やさし絵から、その状況をはっきりとらえさせることが大切である。また、かけ算の意味に立ち戻り、数図ブロックを使った操作をさせてみることも有効である。その際に、図や数図ブロックの操作等を利用して、明確に立式の根拠を説明する活動を取り入れたい。どのような適用題に出会っても、「基準量」「いくつ分」をしっかりとらえられるよう指導したい。

別冊 1 指導資料集49-50頁。

10 かけ算 (2) > 単元の解説 (p.22～p.35)

アレイ図（[●]の図）によるかけ算の表現・・・・・・p.22

 アレイ図(array)とは、下のように[●]（正方形のタイルの中央に丸を配したもの）を縦横に規則正しく並べた図で、6～9の段のかけ算九九を構成するのに、このアレイ図を使っている。

（教科書p.122の図：[●]がタイルのように隙間なく縦9×横9に敷き詰められている。表頭、表側には1から9の数字が対応する[●]の隣に、マイナス記号を取り去った第IV象限のように振られている。）

 アレイ図を操作用紙でかくしながら、右へずらすことによって、[●]の個数が1列、2列、3列・・・と見えていくところにこの図のよさがある。つまり、縦1列の[●]の個数が基準量で、横に何列あるかで、全体の数をとらえさせることができる。やがては、かけ算で[●]の個数を求められるようにしていく。

乗法演算の2つの型・・・・・・p.22

 本単元でアレイ図を使う第1の意図は、前に述べた6～9の段の九九の能率的な構成であるが、第2の意図として、積になる事象にもかけ算が使われることを自然に納得できるようにすることがあげられる。

 乗法の演算の意味には、基本的には2つある。4×3の式の例では、次の2つである。

（教科書p.5より引用：

いくつ分

[1] （図：遊園地の乗り物）は 1台に 4人ずつ のれます。 3台では 何人 のれますか。）

 1つは、上のように、4人の3台分を求めるような場合であり、このときの3は、3倍というはたらきをもった数（オペレータ）である（単項演算）。

 もう1つは、右*のように長方形の形に並んだもの(array)の個数を求める場合で、かけられる数とかける数（この場合は縦の数と横の数）は対等であり、入れかえても成り立つ。この場合の演算の結果を2数a, bの積といっている（二項演算）。

*以下に図示。

● ● ●

● ● ●

● ● ●

● ● ●

この字下げブロックは実際には囲み記事である。

(ア) 単項演算

  ×3

4 → 12 (unary operation)

〈1つの数に1つの数が対応〉

(イ) 二項演算

   ×

(4, 3) → 12 (binary operation)

〈2つの数に1つの数が対応〉

 アレイ図を使った構成では、たとえば右の図**では、前単元とのつながりから、縦1列の6個を基準量とみて、「6個の4つ分」という見方で全体の数をとらえさせることになっているが、「4個の6つ分」ととらえることもできる。もちろんここでは、前者のとらえ方（単項演算）で十分である。

**以下に図示。

 1 2 3 4

1[●][●][●][●]

2[●][●][●][●]

3[●][●][●][●]

4[●][●][●][●]

5[●][●][●][●]

6[●][●][●][●]

 しかし、やがては、6×4でも4×6でも[●]の数が求められることを理解させていこうというわけなのである。教科書p.33の[1]のチョコレートの写真はそういう見方ができる問題である。

（教科書p.33より引用：みかん、チョコレート菓子、花の写真）

二項演算の掛算と単項演算の掛算の相違点が示される。全ての掛算はどちらともみなすことができるから、以下のような指導書の考えは誤謬である。すなわち、二項演算においてのみ積になり（なにが積なるのかはこの段落からは不明）、演算子の前後にある数字を入れかえても（計算が？）成り立つ。また、二項演算の方が単項演算より理解しにくいという証拠は示されていないし、仮に理解のし易さに差異があったとしても、子どもが前者で掛算を理解することを禁止する理由にはならない。

書式の凡例

・下線部は書名、ページ数。

・太字部はサブタイトルまたは小見出し。見出し単位の大小はフォントの大きさで区別し、見出しと章立てなどによって引用箇所をできるだけ正確に特定しようとしたが、記憶が正確でないかもしれない。

・黄色の背景部は引用者によるコメント。